Asuniverso
Advanced Member >PLATINUM PLUS<
Autori Rudi Mathematici: è soprattutto una rivista. Un giornalino che gli autori si immaginano che venga stampato e letto su carta, anche se non sono cosí ingenui da non sospettare che molto spesso questo non accada.
Ogni tanto, dalla fine degli Anni Novanta in poi, spuntano occasionalmente in newsgroup italiani come persone che ci chiedono per quante estrazioni di fila un numero può mancare nelle estrazioni del lotto. O, come direbbero loro, “qual è il ritardo massimo teorico nel lotto?” Qui stiamo parlando del lotto tradizionale, non del Superenalotto.
Ovviamente rispondiamo “non c’è un massimo”, o “infinito”; ma spesso queste persone vogliono sentirsi dire (o dicono loro a noi) che la risposta è 220. Almeno, una ventina di anni fa era 220: forse adesso dicono un altro valore per motivi che diventeranno chiari più tardi.
Se si chiede loro come mai ci dovrebbe essere un limite di 220, dicono che lo afferma la Formula di Samaritani:
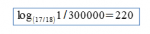
La prima volta che io e altri abbiamo incontrato questa affermazione non ci era esattamente chiaro perché avrebbe dovuto avere alcun senso. Ci è stato detto che 300000 è 50 x 6000. Il che è vero. Il “50” perché nel passato c’erano 10 “ruote” del lotto (e molto tempo fa ce n’erano 8, pare) e in ogni ruota si estraggono 5 numeri. E ovviamente 17/18 appare perché è la probabilità che un dato numero non esca in una data estrazione. Il “6000” perché fino ad una ventina di anni fa c’erano state in tutto circa 6000 estrazioni.
Più generalmente, il “ritardo massimo teorico” sarebbe
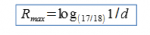
ove d è il “numero di numeri” che sono già stati estratti.
A questo punto uno si può anche interrogare sul significato di “massimo teorico”. Magari non vuol dire quello che sembra voler dire.
Invece di dire “lunghezza di un blocco di assenze” o qualcosa del genere, dirò “ritardo” perché è più breve, nonostante il fatto che l’uso di termini come “ritardo” potrebbe dare l’impressione che il concetto di “ritardo” nelle estrazioni del lotto abbia un qualche senso o utilità.
Forse non tutti, ma almeno alcuni ritardisti seguaci di Samaritani sembrano affermare che, secondo Samaritani, il ritardo massimo possibile dopo che d numeri sono stati estratti è il logaritmo in base 17/18 di d. Questo è palesemente assurdo, e se Samaritani ha veramente detto questo era matto. O magari un truffatore di qualche tipo.
Forse non tutti, ma almeno alcuni ritardisti seguaci di Samaritani affermano pertanto che c’è garanzia di vincere dei soldi facendo questo: Si aspetta che un numero non esca da 160 estrazioni(o, nei loro termini, “abbia un ritardo di 160”);
Visto che secondo la Formula di Samaritani il ritardo massimo possibile è 220, si punta su questo singolo numero (una cosa possibile nel lotto italiano ma, per quel poco che so di queste cose, non in molte altre lotterie); Ogni volta che non esce, si aumenta la scommessa di circa l’11%.
Quando il numero uscirà si rivinceranno tutti i soldi persi fino a questo punto finora e ci si guadagnerà anche qualcosa. Se si hanno più soldi a disposizione, si può anche cominciare con ritardi minori di 160. Visto che un ritardo di 221 sarebbe impossibile in questo universo alternativo, si può calcolare quanti soldi si devono avere a disposizione per poter vincere 10 euro in questo modo. Per cominciare con una scommessa da 1 euro a ritardo 160, bisogna avere qualche migliaio di euro.
C’è da divertirsi con questa idea. Chiamiamo questo divertimento “lo sfottimento tramite la partecipazione”: se più numeri raggiungono un ritardo di 220 (sulla stessa ruota) insieme, dovranno uscire insieme perché un ritardo di 221 è impossibile. Ma cosa succede se 6 numeri arrivano ad un ritardo di 220 insieme? Questo deve essere impossibile. Allora uno di questi deve uscire prima. Andiamo un po’ oltre: con le dovute estrazioni possiamo fare in modo che, grazie al potere mistico della Formula di Samaritani, si potranno prevedere 17 cinquine di fila! Se gli stessi cinque numeri escono 204 volte di fila e le estrazioni passate sono tali che fra i numeri restanti ci sono 5 con ritardo 220, 5 con 519, ..., e 5 con 204, le prossime 17 cinquine sono obbligate.
Per motivi a me incomprensibili, i ritardisti sembrano offendersi se dici loro queste cose; ma se offrono un modello balordo del lotto, è doveroso esplorare le conseguenze assurde del modello. In passato, quando un numero ha raggiunto un “ritardo” molto alto, mi sembra di aver capito che almeno qualcuno si è rovinato o suicidato. Non posso dare tutta la colpa ai ritardisti: anche la stampa sembra dare l’impressione che i ritardi abbiano un qualche significato. Sto pensando, per esempio, al caso del 53 a Venezia nel 2005.
Chiaramente, la Formula di Samaritani così come è presentata dai ritardisti è una balla. E uno potrebbe benissimo fermarsi qui dicendo “Se le estrazioni sono indipendenti, questo è palesemente assurdo. Avanti il prossimo.” Ma è opportuno tenere presente che i ritardisti non dicono soltanto cose false. Possono anche dire cose vere ma irrilevanti. Per esempio citano la Legge dei Grandi Numeri e il Teorema del Limite Centrale.
Simuliamo 6000 estrazioni di un gioco del lotto con 10 ruote e vediamo quant’è il ritardo più lungo. Facciamolo più volte per vedere com’è la distribuzione del massimo ritardo. Magari 220 è un valore insolitamente alto? Evidentemente il massimo ritardo potrebbe essere qualsiasi cosa da 17 a 6000 anche se 17 e 6000 sarebbero entrambi molto rari.
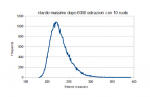
Sorpresa: 220 era il valore più comune! C’è un elemento di fortuna, forse: durante la simulazione altri valori da 221 a 226 sono stati i più comuni per un po’. La mediana qui è 226, la media è 229 a meno di qualche decimale, e lo scarto quadratico medio è circa 22,2. Il valore 220 non sembra particolarmente alto. Se Samaritani o i ritardisti vogliono ingannare qualcuno con una finta soglia invalicabile, non dovrebbe essere come minimo un valore raggiunto raramente nelle simulazioni? Non hanno mai controllato?
Modelli del lotto
Quando ho insistito, i ritardisti che ho incontrato (virtualmente) sembravano affermare che le estrazioni del lotto sono indipendenti e che tutte le combinazioni hanno la stessa probabilità di uscita. Curioso... confesso che se volessi fare il ritardista andrei in giro dicendo che le estrazioni non sono indipendenti: sembrerei eccentrico, certo, ma essere un ritardista che afferma che le estrazioni sono indipendenti implica essere o stupido o truffatore, che mi sembra peggio.
Comunque, non è impossibile che il gioco del Lotto abbia difetti tali che le cinquine abbiano probabilità diverse, o che le estrazioni non siano indipendenti. Quando ho incontrato per la prima volta il fenomeno dei ritardisti e la Formula di Samaritani, le estrazioni venivano ancora fatte a mano da bambini. Bambini orfani, se ho capito bene. Le palle erano inserite in un qualche meccanismo in un ordine specifico: mischiate un po’, quindi veniva estratto il primo numero; poi le palline erano mischiate un altro po’, eccetera.
C’era chi sosteneva che la distribuzione del primo numero non fosse uniforme. Questo non sembra del tutto implausibile. Ma così poco uniforme da rendere il gioco tale che qualcuno riesca a trarne vantaggio? Inverosimile. Se le estrazioni sono indipendenti ma i numeri hanno probabilità diverse, in realtà i ritardisti hanno più torto che mai, in quanto i numeri meno probabili arriveranno solitamente a ritardi maggiori, e giocarli peggiorerà le possibilità di vincere. Ma in quasi tutto questo articolo do per scontato che stiamo usando il modello naturale in cui le estrazioni sono indipendenti e ogni cinquina ha la stessa probabilità di uscire.
Partendo da questo presupposto, però, è possibile creare un gioco del lotto con estrazioni non indipendenti! Inseriamo le palle nell’ordine dei loro ritardi, mischiamo poco e male, usiamo solo orfani con braccia corte, e via di questo passo. Si potrebbe fare in modo che i numeri più “ritardanti” diventino più probabili. Masi potrebbe anche fare in modo che i numeri appena usciti diventino più probabili! Questo sarebbe più divertente.
Ma anche in questo caso, avvantaggiando in qualche modo i numeri con ritardo maggiore, non è chiaro come potrebbe importare “quanto” fosse il ritardo maggiore. Chiaramente se qualcuno afferma sia che le estrazioni sono indipendenti e le cinquine sono equiprobabili, sia che uno studio dei ritardi è utile, questo qualcuno è o folle o truffatore. O ignorante, o qualcuno che non pensa a quello che dice; ma se qualcuno dice che studia i ritardi fin da prima della mia nascita, allora è proprio negato, e definirlo matto mi sembra pienamente giustificato. Uno che non capisce l’indipendenza degli eventi dopo cinquanta anni di studio ha seri problemi. Ascoltare quello che ha da dire lui sulla teoria delle probabilità è come chiedere a me come funzionano i sottogruppi normali.
È forse possibile che i ritardisti, come alcuni dei personaggi nei libri di Smullyan, credano di credere che le estrazioni siano indipendenti, ma in realtà credono che non lo siano. Però non è una cosa che vogliono sentirsi dire. Torniamo alla nostra simulazione. Proviamo vari numeri di estrazioni per un gioco del lotto con 11 ruote e vediamo cosa succede: qui vediamo il “numero di Samaritani” per numeri di estrazioni da 1 a circa 10 milioni. Vediamo anche alcuni dati sulla distribuzione del massimo ritardo in tot estrazioni del lotto a 11 ruote: la media, la moda, la mediana e lo scarto quadratico medio della distribuzione.
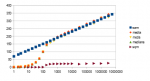
Per numeri bassi di estrazioni, Samaritani fornisce un numero impossibilmente alto, ma per numeri da qualche centinaio in su, tutti gli indici di tendenza centrale e il numero di Samaritani sono più o meno uguali. Quindi viene il sospetto che Samaritani volesse stimare il massimo ritardo, e non trovare una soglia “invalicabile”. Questo vorrebbe dire che i ritardisti moderni non capiscono quello che diceva, o che fingono di non capire per ingannare meglio i creduloni. Io almeno sono rimasto sorpreso nel vedere che lo scarto quadratico medio non sembra variare col numero di estrazioni.
Dani Ferrari, menzionato prima, è andato alla Biblioteca Nazionale a Roma a cercare il libro di Samaritani, “La teoria e il calcolo matematico dei ritardi. Studio teorico e pratico sul giuoco del Lotto” del 1937. (“Giuoco”? Retrò! Ma ok, Samaritani l’ha scritto nel 1937 quindi lasciamo stare). Dani ha concluso che, come immaginavamo, Samaritani non era né scemo né truffatore, ma voleva stimare il massimo ritardo; non intendeva trovare un valore oltre il quale non fosse possibile andare. Magari in uno dei prossimi decenni cercherò di comprare questo libro: ma sembra difficile da trovare.
Come possiamo derivare la Formula di Samaritani?
Per cominciare, possiamo trattare un singolo numero del lotto come una moneta sbilanciata: una moneta che, una volta lanciata, mostri “testa” (il numero esce) con probabilità p = 1/18, e “croce” (il numero non esce) con probabilità q = 17/18. Chiediamoci cosa si possa dire sulla lunghezza del blocco più lungo di croci.
A quanto pare è un risultato noto che il blocco più lungo di croci ha lunghezza media data da:
logﯠ ( 1 / np )
Come si ottiene questo risultato? Usiamo un po’ di spannometria. Avremo circa npteste e quindi circa npblocchi di croci. (Non ci preoccupiamo più di tanto di +/–1 qui, stiamo facendo la spannometria). Diciamo esattamente np blocchi di croci.
A questo punto possiamo procedere in almeno due modi.
Modo I – Scriviamo la probabilità che un’osservazione da una distribuzione geometrica con media 18 sia ≤k. Eleviamo questo valore alla np-esima per ottenere la probabilità che np osservazioni siano tutte ≤k. Va bene, non sono indipendenti perché c’è un vincolo sulla somma, eccetera, ma andiamo avanti. Prendiamo la derivata rispetto a k per ottenere la densità. Deriviamo rispetto a k di nuovo, e vediamo per quale valore di k è 0. Questo valore sarà la moda.
Modo II – Consideriamo un elenco dei valori delle lunghezze dei blocchi di croci: 1/18 di questi numeri sarà 0;; 17/18²
sarà 1, ecc. Ci chiediamo quale sia il valore tale che avremo mediamente Un blocco di lunghezza maggiore o uguale a quel valore.
In entrambi i casi otteniamo
logﯠ ( 1 / np )
o qualcosa di molto simile
Come possiamo estendere questo ad un lotto con 11 ruote? Chiaramente i numeri non sono indipendenti. Esattamente cinque numeri in una data ruota escono ad ogni estrazione. Ma visto che stiamo facendo spannometria, sorvoliamo. Trattiamo le 11 ruote del lotto come 990 monete indipendenti, lanciate n volte in parallelo. Ma a questo punto tanto vale trattare il lotto come 990 n lanci di una sola moneta. Chiaramente questo permetterebbe “ritardi” maggiori di n, e farebbe contare come un ritardo singolo un blocco di croci alla fine di un gruppo di n accanto al prossimo gruppo di n, ma per n abbastanza grande ce ne freghiamo.
Col metodo (I) la Formula di Samaritani spunta subito!
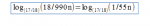
Come sospettavamo, la Formula di Samaritani stima il massimo ritardo, e non un limite al valore più alto che questo può avere (che è ovviamente n dopo n lanci o infinito in generale). Questo risultato sul massimo blocco di croci in n lanci di una moneta sbilanciata si conosceva prima del 1937? Sembra possibile, ma non lo so. Col metodo (II) abbiamo esattamente 55 n“successi” e di nuovo la Formula di Samaritani spunta subito. Chiaramente, c’è il problema che i primi 55 numeri sono tutti 0, i successivi 55 sono al massimo 1, ecc. ma per n abbastanza grande ce ne freghiamo di nuovo.
Come migliorare la Formula di Samaritani?
Ovviamente, la Formula di Samaritani è completamente inutile per giocare al lotto, ma se vogliamo qualcosa che funzioni meglio per n basso (sempre inutile per giocare a lotto, però) possiamo fare come ha fatto Francesco Romani. Calcoliamo la distribuzione esatta del “ritardo massimo” di una singola moneta lanciata n volte invece di approssimare, come abbiamo fatto, con il nostro “diciamo che esca testa np volte”.
Consideriamo un singolo numero nel lotto (o moneta sbilanciata): p = 1/18, q = 17/18
Definiamo
G ( n , r )
come la probabilità che dopo n lanci/estrazioni si è verificato un ritardo r Avremo:
g ( n , r ) = 0
per n < r, e
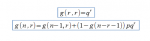
per n > r.
Questo perché se abbiamo visto un ritardo r dopo n estrazioni, o l’avevamo già visto dopo n – 1 estrazioni, o abbiamo avuto n– 1 – r estrazioni senza ritardo r, poi un’uscita, poi un ritardo di r. La probabilità che dopo n estrazioni il ritardo massimo sia esattamente r è dato da
g(n, r) – g(n, r+1)
Come abbiamo fatto prima, per passare all’intero “lotto” con tutte le sue estrazioni e ruote, prendiamo la versione cumulativa di questo per avere la probabilità del massimo ritardo minore o uguale a r, e prendiamo la 990 esima potenza per avere la probabilità del massimo ritardo in tutto il lotto minore o uguale a r(ignorando il fatto che i numeri non sono tutti indipendenti fra di loro in una singola estrazione in una singola ruota).
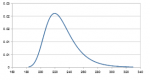
Ecco un grafico della distribuzione del massimo ritardo usando la tecnica di Romani per 6000 estrazioni di una lotteria a 10 ruote (quindi 900-esima potenza non 990-esima). La moda è 220.
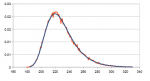
Aggiungiamo le simulazioni che abbiamo fatto prima: per i nostri scopi, questo sembra ottimo.
È divertente notare che per n basso, la distribuzione del massimo ritardo è bimodale. Per esempio, per n = 178 e 11 ruote, si ha il grafico seguente:
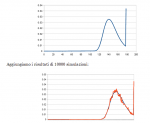
Ottimo, di nuovo. Per n = 100, si vede quasi soltanto la moda a n = 100.
Centenari Qualcuno parla dei “centenari” (numeri con ritardo oltre 100) come se fossero speciali. Sono almeno abbastanza rari da essere notevoli? Facciamo un grafico del massimo ritardo attualmente presente per 10000 estrazioni e vediamo cosa succede:

Avere almeno un numero con un ritardo oltre 100 sembra abbastanza normale. Una domanda ragionevole può essere “Come fa la Formula di Samaritani ad essere una truffa se te la regalano?” Magari questo ci spinge a presumere che è più probabile che i ritardisti siano sciocchi anziché truffatori. Ma forse la Formula di Samaritani serve come articolo civetta, o campione gratis, e vogliono venderti riviste, software, previsioni personalizzate. Magari vogliono dirti che ci sono tipi di ritardi più sofisticati o avanzati. Ritardi di livello, ritardi compensati, ritardi all’aglio, olio e peperoncino. Chiaramente, la riposta come sempre è “Le estrazioni sono indipendenti? Sì? Allora sei scemo o truffatore. Avanti il prossimo.”
Conclusioni
La conclusione finale è che la Formula di Samaritani non è balorda e che Samaritani probabilmente non era uno sciocco. Sono i suoi seguaci moderni ad esserlo (o sono truffatori), loro che usano una formula basata sulla supposizione che gli eventi sono indipendenti per cercare di dire che non lo sono. Non avendo visto il libro personalmente non posso essere sicuro che Samaritani non fosse un ritardista, ma Dani Ferrari non è affatto sciocco e sono dispostissimo a fidarmi di lui.
Continua ad essere probabile che chi parla della Formula di Samaritani è probabilmente in malafede o poco intelligente. Faccio eccezione per me stesso nel contesto di questo articolo, ovviamente. Usare un altro termine (per esempio, quello del risultato di base per la singola moneta) potrebbe essere meglio se non vuoi essere preso per folle. Lo stesso metodo di “trattare i numeri come indipendenti anche sapendo che non lo sono” sembra funzionare abbastanza bene anche per lanci di un dado, per numeri decimali casuali, ecc. (Una specie di lotto a ruota singola dove un numero viene estratto tra 6 o 10 possibilità).
Mentre la formula di Samaritani è inutile per il Lotto come funziona realmente, magari se qualcuno dice “Sto per lanciare un nuovo gioco del Lotto esattamente come quello normale. Volete scommettere su quanto sarà stato il massimo ritardo fra 100 anni?” potrebbe avere una qualche utilità ma si dovrebbero conoscere i termini precisi della scommessa.
Lo scopo di questo articolo è in parte:
a) aiutare chi si trova a lottare con le scemenze dei ritardisti;
b) mostrare che la Formula di Samaritani non è assurda come potrebbe sembrare, ma che i ritardisti (magari volutamente) non sembrano capirla. È un peccato che il nome di Samaritani sia infangato ingiustamente dai ritardisti.
Saluti...
Ogni tanto, dalla fine degli Anni Novanta in poi, spuntano occasionalmente in newsgroup italiani come persone che ci chiedono per quante estrazioni di fila un numero può mancare nelle estrazioni del lotto. O, come direbbero loro, “qual è il ritardo massimo teorico nel lotto?” Qui stiamo parlando del lotto tradizionale, non del Superenalotto.
Ovviamente rispondiamo “non c’è un massimo”, o “infinito”; ma spesso queste persone vogliono sentirsi dire (o dicono loro a noi) che la risposta è 220. Almeno, una ventina di anni fa era 220: forse adesso dicono un altro valore per motivi che diventeranno chiari più tardi.
Se si chiede loro come mai ci dovrebbe essere un limite di 220, dicono che lo afferma la Formula di Samaritani:
La prima volta che io e altri abbiamo incontrato questa affermazione non ci era esattamente chiaro perché avrebbe dovuto avere alcun senso. Ci è stato detto che 300000 è 50 x 6000. Il che è vero. Il “50” perché nel passato c’erano 10 “ruote” del lotto (e molto tempo fa ce n’erano 8, pare) e in ogni ruota si estraggono 5 numeri. E ovviamente 17/18 appare perché è la probabilità che un dato numero non esca in una data estrazione. Il “6000” perché fino ad una ventina di anni fa c’erano state in tutto circa 6000 estrazioni.
Più generalmente, il “ritardo massimo teorico” sarebbe
ove d è il “numero di numeri” che sono già stati estratti.
A questo punto uno si può anche interrogare sul significato di “massimo teorico”. Magari non vuol dire quello che sembra voler dire.
Invece di dire “lunghezza di un blocco di assenze” o qualcosa del genere, dirò “ritardo” perché è più breve, nonostante il fatto che l’uso di termini come “ritardo” potrebbe dare l’impressione che il concetto di “ritardo” nelle estrazioni del lotto abbia un qualche senso o utilità.
Forse non tutti, ma almeno alcuni ritardisti seguaci di Samaritani sembrano affermare che, secondo Samaritani, il ritardo massimo possibile dopo che d numeri sono stati estratti è il logaritmo in base 17/18 di d. Questo è palesemente assurdo, e se Samaritani ha veramente detto questo era matto. O magari un truffatore di qualche tipo.
Forse non tutti, ma almeno alcuni ritardisti seguaci di Samaritani affermano pertanto che c’è garanzia di vincere dei soldi facendo questo: Si aspetta che un numero non esca da 160 estrazioni(o, nei loro termini, “abbia un ritardo di 160”);
Visto che secondo la Formula di Samaritani il ritardo massimo possibile è 220, si punta su questo singolo numero (una cosa possibile nel lotto italiano ma, per quel poco che so di queste cose, non in molte altre lotterie); Ogni volta che non esce, si aumenta la scommessa di circa l’11%.
Quando il numero uscirà si rivinceranno tutti i soldi persi fino a questo punto finora e ci si guadagnerà anche qualcosa. Se si hanno più soldi a disposizione, si può anche cominciare con ritardi minori di 160. Visto che un ritardo di 221 sarebbe impossibile in questo universo alternativo, si può calcolare quanti soldi si devono avere a disposizione per poter vincere 10 euro in questo modo. Per cominciare con una scommessa da 1 euro a ritardo 160, bisogna avere qualche migliaio di euro.
C’è da divertirsi con questa idea. Chiamiamo questo divertimento “lo sfottimento tramite la partecipazione”: se più numeri raggiungono un ritardo di 220 (sulla stessa ruota) insieme, dovranno uscire insieme perché un ritardo di 221 è impossibile. Ma cosa succede se 6 numeri arrivano ad un ritardo di 220 insieme? Questo deve essere impossibile. Allora uno di questi deve uscire prima. Andiamo un po’ oltre: con le dovute estrazioni possiamo fare in modo che, grazie al potere mistico della Formula di Samaritani, si potranno prevedere 17 cinquine di fila! Se gli stessi cinque numeri escono 204 volte di fila e le estrazioni passate sono tali che fra i numeri restanti ci sono 5 con ritardo 220, 5 con 519, ..., e 5 con 204, le prossime 17 cinquine sono obbligate.
Per motivi a me incomprensibili, i ritardisti sembrano offendersi se dici loro queste cose; ma se offrono un modello balordo del lotto, è doveroso esplorare le conseguenze assurde del modello. In passato, quando un numero ha raggiunto un “ritardo” molto alto, mi sembra di aver capito che almeno qualcuno si è rovinato o suicidato. Non posso dare tutta la colpa ai ritardisti: anche la stampa sembra dare l’impressione che i ritardi abbiano un qualche significato. Sto pensando, per esempio, al caso del 53 a Venezia nel 2005.
Chiaramente, la Formula di Samaritani così come è presentata dai ritardisti è una balla. E uno potrebbe benissimo fermarsi qui dicendo “Se le estrazioni sono indipendenti, questo è palesemente assurdo. Avanti il prossimo.” Ma è opportuno tenere presente che i ritardisti non dicono soltanto cose false. Possono anche dire cose vere ma irrilevanti. Per esempio citano la Legge dei Grandi Numeri e il Teorema del Limite Centrale.
Simuliamo 6000 estrazioni di un gioco del lotto con 10 ruote e vediamo quant’è il ritardo più lungo. Facciamolo più volte per vedere com’è la distribuzione del massimo ritardo. Magari 220 è un valore insolitamente alto? Evidentemente il massimo ritardo potrebbe essere qualsiasi cosa da 17 a 6000 anche se 17 e 6000 sarebbero entrambi molto rari.

Sorpresa: 220 era il valore più comune! C’è un elemento di fortuna, forse: durante la simulazione altri valori da 221 a 226 sono stati i più comuni per un po’. La mediana qui è 226, la media è 229 a meno di qualche decimale, e lo scarto quadratico medio è circa 22,2. Il valore 220 non sembra particolarmente alto. Se Samaritani o i ritardisti vogliono ingannare qualcuno con una finta soglia invalicabile, non dovrebbe essere come minimo un valore raggiunto raramente nelle simulazioni? Non hanno mai controllato?
Modelli del lotto
Quando ho insistito, i ritardisti che ho incontrato (virtualmente) sembravano affermare che le estrazioni del lotto sono indipendenti e che tutte le combinazioni hanno la stessa probabilità di uscita. Curioso... confesso che se volessi fare il ritardista andrei in giro dicendo che le estrazioni non sono indipendenti: sembrerei eccentrico, certo, ma essere un ritardista che afferma che le estrazioni sono indipendenti implica essere o stupido o truffatore, che mi sembra peggio.
Comunque, non è impossibile che il gioco del Lotto abbia difetti tali che le cinquine abbiano probabilità diverse, o che le estrazioni non siano indipendenti. Quando ho incontrato per la prima volta il fenomeno dei ritardisti e la Formula di Samaritani, le estrazioni venivano ancora fatte a mano da bambini. Bambini orfani, se ho capito bene. Le palle erano inserite in un qualche meccanismo in un ordine specifico: mischiate un po’, quindi veniva estratto il primo numero; poi le palline erano mischiate un altro po’, eccetera.
C’era chi sosteneva che la distribuzione del primo numero non fosse uniforme. Questo non sembra del tutto implausibile. Ma così poco uniforme da rendere il gioco tale che qualcuno riesca a trarne vantaggio? Inverosimile. Se le estrazioni sono indipendenti ma i numeri hanno probabilità diverse, in realtà i ritardisti hanno più torto che mai, in quanto i numeri meno probabili arriveranno solitamente a ritardi maggiori, e giocarli peggiorerà le possibilità di vincere. Ma in quasi tutto questo articolo do per scontato che stiamo usando il modello naturale in cui le estrazioni sono indipendenti e ogni cinquina ha la stessa probabilità di uscire.
Partendo da questo presupposto, però, è possibile creare un gioco del lotto con estrazioni non indipendenti! Inseriamo le palle nell’ordine dei loro ritardi, mischiamo poco e male, usiamo solo orfani con braccia corte, e via di questo passo. Si potrebbe fare in modo che i numeri più “ritardanti” diventino più probabili. Masi potrebbe anche fare in modo che i numeri appena usciti diventino più probabili! Questo sarebbe più divertente.
Ma anche in questo caso, avvantaggiando in qualche modo i numeri con ritardo maggiore, non è chiaro come potrebbe importare “quanto” fosse il ritardo maggiore. Chiaramente se qualcuno afferma sia che le estrazioni sono indipendenti e le cinquine sono equiprobabili, sia che uno studio dei ritardi è utile, questo qualcuno è o folle o truffatore. O ignorante, o qualcuno che non pensa a quello che dice; ma se qualcuno dice che studia i ritardi fin da prima della mia nascita, allora è proprio negato, e definirlo matto mi sembra pienamente giustificato. Uno che non capisce l’indipendenza degli eventi dopo cinquanta anni di studio ha seri problemi. Ascoltare quello che ha da dire lui sulla teoria delle probabilità è come chiedere a me come funzionano i sottogruppi normali.
È forse possibile che i ritardisti, come alcuni dei personaggi nei libri di Smullyan, credano di credere che le estrazioni siano indipendenti, ma in realtà credono che non lo siano. Però non è una cosa che vogliono sentirsi dire. Torniamo alla nostra simulazione. Proviamo vari numeri di estrazioni per un gioco del lotto con 11 ruote e vediamo cosa succede: qui vediamo il “numero di Samaritani” per numeri di estrazioni da 1 a circa 10 milioni. Vediamo anche alcuni dati sulla distribuzione del massimo ritardo in tot estrazioni del lotto a 11 ruote: la media, la moda, la mediana e lo scarto quadratico medio della distribuzione.

Per numeri bassi di estrazioni, Samaritani fornisce un numero impossibilmente alto, ma per numeri da qualche centinaio in su, tutti gli indici di tendenza centrale e il numero di Samaritani sono più o meno uguali. Quindi viene il sospetto che Samaritani volesse stimare il massimo ritardo, e non trovare una soglia “invalicabile”. Questo vorrebbe dire che i ritardisti moderni non capiscono quello che diceva, o che fingono di non capire per ingannare meglio i creduloni. Io almeno sono rimasto sorpreso nel vedere che lo scarto quadratico medio non sembra variare col numero di estrazioni.
Dani Ferrari, menzionato prima, è andato alla Biblioteca Nazionale a Roma a cercare il libro di Samaritani, “La teoria e il calcolo matematico dei ritardi. Studio teorico e pratico sul giuoco del Lotto” del 1937. (“Giuoco”? Retrò! Ma ok, Samaritani l’ha scritto nel 1937 quindi lasciamo stare). Dani ha concluso che, come immaginavamo, Samaritani non era né scemo né truffatore, ma voleva stimare il massimo ritardo; non intendeva trovare un valore oltre il quale non fosse possibile andare. Magari in uno dei prossimi decenni cercherò di comprare questo libro: ma sembra difficile da trovare.
Come possiamo derivare la Formula di Samaritani?
Per cominciare, possiamo trattare un singolo numero del lotto come una moneta sbilanciata: una moneta che, una volta lanciata, mostri “testa” (il numero esce) con probabilità p = 1/18, e “croce” (il numero non esce) con probabilità q = 17/18. Chiediamoci cosa si possa dire sulla lunghezza del blocco più lungo di croci.
A quanto pare è un risultato noto che il blocco più lungo di croci ha lunghezza media data da:
logﯠ ( 1 / np )
Come si ottiene questo risultato? Usiamo un po’ di spannometria. Avremo circa npteste e quindi circa npblocchi di croci. (Non ci preoccupiamo più di tanto di +/–1 qui, stiamo facendo la spannometria). Diciamo esattamente np blocchi di croci.
A questo punto possiamo procedere in almeno due modi.
Modo I – Scriviamo la probabilità che un’osservazione da una distribuzione geometrica con media 18 sia ≤k. Eleviamo questo valore alla np-esima per ottenere la probabilità che np osservazioni siano tutte ≤k. Va bene, non sono indipendenti perché c’è un vincolo sulla somma, eccetera, ma andiamo avanti. Prendiamo la derivata rispetto a k per ottenere la densità. Deriviamo rispetto a k di nuovo, e vediamo per quale valore di k è 0. Questo valore sarà la moda.
Modo II – Consideriamo un elenco dei valori delle lunghezze dei blocchi di croci: 1/18 di questi numeri sarà 0;; 17/18²
sarà 1, ecc. Ci chiediamo quale sia il valore tale che avremo mediamente Un blocco di lunghezza maggiore o uguale a quel valore.
In entrambi i casi otteniamo
logﯠ ( 1 / np )
o qualcosa di molto simile
Come possiamo estendere questo ad un lotto con 11 ruote? Chiaramente i numeri non sono indipendenti. Esattamente cinque numeri in una data ruota escono ad ogni estrazione. Ma visto che stiamo facendo spannometria, sorvoliamo. Trattiamo le 11 ruote del lotto come 990 monete indipendenti, lanciate n volte in parallelo. Ma a questo punto tanto vale trattare il lotto come 990 n lanci di una sola moneta. Chiaramente questo permetterebbe “ritardi” maggiori di n, e farebbe contare come un ritardo singolo un blocco di croci alla fine di un gruppo di n accanto al prossimo gruppo di n, ma per n abbastanza grande ce ne freghiamo.
Col metodo (I) la Formula di Samaritani spunta subito!
Come sospettavamo, la Formula di Samaritani stima il massimo ritardo, e non un limite al valore più alto che questo può avere (che è ovviamente n dopo n lanci o infinito in generale). Questo risultato sul massimo blocco di croci in n lanci di una moneta sbilanciata si conosceva prima del 1937? Sembra possibile, ma non lo so. Col metodo (II) abbiamo esattamente 55 n“successi” e di nuovo la Formula di Samaritani spunta subito. Chiaramente, c’è il problema che i primi 55 numeri sono tutti 0, i successivi 55 sono al massimo 1, ecc. ma per n abbastanza grande ce ne freghiamo di nuovo.
Come migliorare la Formula di Samaritani?
Ovviamente, la Formula di Samaritani è completamente inutile per giocare al lotto, ma se vogliamo qualcosa che funzioni meglio per n basso (sempre inutile per giocare a lotto, però) possiamo fare come ha fatto Francesco Romani. Calcoliamo la distribuzione esatta del “ritardo massimo” di una singola moneta lanciata n volte invece di approssimare, come abbiamo fatto, con il nostro “diciamo che esca testa np volte”.
Consideriamo un singolo numero nel lotto (o moneta sbilanciata): p = 1/18, q = 17/18
Definiamo
G ( n , r )
come la probabilità che dopo n lanci/estrazioni si è verificato un ritardo r Avremo:
g ( n , r ) = 0
per n < r, e
per n > r.
Questo perché se abbiamo visto un ritardo r dopo n estrazioni, o l’avevamo già visto dopo n – 1 estrazioni, o abbiamo avuto n– 1 – r estrazioni senza ritardo r, poi un’uscita, poi un ritardo di r. La probabilità che dopo n estrazioni il ritardo massimo sia esattamente r è dato da
g(n, r) – g(n, r+1)
Come abbiamo fatto prima, per passare all’intero “lotto” con tutte le sue estrazioni e ruote, prendiamo la versione cumulativa di questo per avere la probabilità del massimo ritardo minore o uguale a r, e prendiamo la 990 esima potenza per avere la probabilità del massimo ritardo in tutto il lotto minore o uguale a r(ignorando il fatto che i numeri non sono tutti indipendenti fra di loro in una singola estrazione in una singola ruota).

Ecco un grafico della distribuzione del massimo ritardo usando la tecnica di Romani per 6000 estrazioni di una lotteria a 10 ruote (quindi 900-esima potenza non 990-esima). La moda è 220.

Aggiungiamo le simulazioni che abbiamo fatto prima: per i nostri scopi, questo sembra ottimo.
È divertente notare che per n basso, la distribuzione del massimo ritardo è bimodale. Per esempio, per n = 178 e 11 ruote, si ha il grafico seguente:

Ottimo, di nuovo. Per n = 100, si vede quasi soltanto la moda a n = 100.
Centenari Qualcuno parla dei “centenari” (numeri con ritardo oltre 100) come se fossero speciali. Sono almeno abbastanza rari da essere notevoli? Facciamo un grafico del massimo ritardo attualmente presente per 10000 estrazioni e vediamo cosa succede:

Avere almeno un numero con un ritardo oltre 100 sembra abbastanza normale. Una domanda ragionevole può essere “Come fa la Formula di Samaritani ad essere una truffa se te la regalano?” Magari questo ci spinge a presumere che è più probabile che i ritardisti siano sciocchi anziché truffatori. Ma forse la Formula di Samaritani serve come articolo civetta, o campione gratis, e vogliono venderti riviste, software, previsioni personalizzate. Magari vogliono dirti che ci sono tipi di ritardi più sofisticati o avanzati. Ritardi di livello, ritardi compensati, ritardi all’aglio, olio e peperoncino. Chiaramente, la riposta come sempre è “Le estrazioni sono indipendenti? Sì? Allora sei scemo o truffatore. Avanti il prossimo.”
Conclusioni
La conclusione finale è che la Formula di Samaritani non è balorda e che Samaritani probabilmente non era uno sciocco. Sono i suoi seguaci moderni ad esserlo (o sono truffatori), loro che usano una formula basata sulla supposizione che gli eventi sono indipendenti per cercare di dire che non lo sono. Non avendo visto il libro personalmente non posso essere sicuro che Samaritani non fosse un ritardista, ma Dani Ferrari non è affatto sciocco e sono dispostissimo a fidarmi di lui.
Continua ad essere probabile che chi parla della Formula di Samaritani è probabilmente in malafede o poco intelligente. Faccio eccezione per me stesso nel contesto di questo articolo, ovviamente. Usare un altro termine (per esempio, quello del risultato di base per la singola moneta) potrebbe essere meglio se non vuoi essere preso per folle. Lo stesso metodo di “trattare i numeri come indipendenti anche sapendo che non lo sono” sembra funzionare abbastanza bene anche per lanci di un dado, per numeri decimali casuali, ecc. (Una specie di lotto a ruota singola dove un numero viene estratto tra 6 o 10 possibilità).
Mentre la formula di Samaritani è inutile per il Lotto come funziona realmente, magari se qualcuno dice “Sto per lanciare un nuovo gioco del Lotto esattamente come quello normale. Volete scommettere su quanto sarà stato il massimo ritardo fra 100 anni?” potrebbe avere una qualche utilità ma si dovrebbero conoscere i termini precisi della scommessa.
Lo scopo di questo articolo è in parte:
a) aiutare chi si trova a lottare con le scemenze dei ritardisti;
b) mostrare che la Formula di Samaritani non è assurda come potrebbe sembrare, ma che i ritardisti (magari volutamente) non sembrano capirla. È un peccato che il nome di Samaritani sia infangato ingiustamente dai ritardisti.
Saluti...




