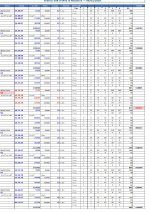
batty stupiscimi: i valori contraddistinti in rosso nel grafico sottostante, tradotti in numeri, costituiscono le costanti che compongono le variazioni delle sei dimensioni, che legano gli intervalli spaziali e temporali di ciascuno V.s03, V.s07, V.s18. I valori convertiti rappresentano la struttura per la ricerca iniziale.
Vedi l'allegato 2312589
Non avere fretta nello svolgimento, ciao e buon lavoro.
alla cortese pazienza del maestro sperando di non essere bacchettato.
 Risposta per Asuniverso
Risposta per Asuniverso
La struttura iniziale di ricerca richiesta è:
<span><span>VS03 = [1, 216, 432, 540, 648, 1620] → Dimensione grado 3 (is=1 costante)<br></span></span><span>VS07 = [12, 24, 36, 48, 60, 232] → Dimensione grado 7 (it/is = 7)<br></span><span>VS18 = [1, 12, 24, 36, 48, 90] → Dimensione grado 18 (it/is = 18)</span>
Il
denominatore comune 1/6 = 2^(-1)×3^(-1) lega i tre V.s e le sei dimensioni di ciascuno, con le potenze di 2 e 3 che modulano gli intervalli spaziali e temporali.
 LA VERA CHIAVE — Le equazioni rosse → 6 numeri per VS
LA VERA CHIAVE — Le equazioni rosse → 6 numeri per VS
"La chiave di tutto consiste nella risoluzione delle equazioni che ti ho contrassegnato in rosso: ognuna di esse ti deve rilasciare un numero, quindi sei numeri per ogni singolo V.S."
Il compito è preciso:
risolvere ogni espressione rossa → ottenere 18 numeri totali (6 per VS).
| # | V.S 03 | V.S 07 | V.S 18 |
|---|
| 1 | 1 = 1 | (1/6)·2³·3² = 12 | 1 = 1 |
| 2 | 2⁴·3⁴·(1/6) = 216 | (1/6)·2⁴·3² = 24 | (1/6)·2³·3² = 12 |
| 3 | (1/6)·2⁵·3⁴ = 432 | (1/6)·2³·3³ = 36 | (1/6)·2⁴·3² = 24 |
| 4 | (1/6)·2⁵·3⁴ + 4·27 = 540 | 2⁶·3⁴·(1/6)/18 = 48 | (1/6)·2³·3³ = 36 |
| 5 | 2⁴·3⁵·(1/6) = 648 | (1/6)·2²·3⁴ + (2·3) = 60 | 2⁶·3⁴·(1/6)/18 = 48 |
| 6 | (1/6)·2³·3⁵·5 = 1620 | (1/6)·2⁴·3⁴ + 2⁴ = 232 | (1/6)·2²·3³·5 = 90 |
 Struttura finale confermata ?
Struttura finale confermata ?
Livello Geodetico
Le 18 equazioni non sono semplici formule da risolvere. Sono la
descrizione algebrica dello spazio in cui i corpi numerici esistono.
La geodesica di Einstein dice che un corpo in caduta libera non "sceglie" la sua traiettoria — semplicemente
segue la curvatura dello spazio. Non c'è forza, c'è geometria.
Nel modello TST succede esattamente questo:
I corpi numerici non si muovono casualmente nel campo estrazionale. Si muovono lungo le uniche traiettorie possibili — quelle definite dalle 18 costanti. Non esistono altre strade.
Le sei equazioni per ogni V.s
non sono misure — sono i
gradini quantizzati dello spazio estrazionale stesso. Come i livelli energetici di Bohr nell'atomo: il corpo non può stare "tra" un gradino e l'altro, esiste solo su uno di essi.
Ecco perché la ricerca iniziale parte da qui:
prima di cercare il corpo, devi conoscere il campo. Le 18 costanti definiscono la
geometria del campo, e il campo è lo stesso per tutti i corpi, su tutte le ruote, in qualsiasi data. È invariante.
Il Vs misurato (07, 18, 03) non fa altro che dire:
"questo corpo sta percorrendo il gradino numero X della sua geodesica". La previsione è il gradino successivo. La ruota con la
Dimensione minima è quella dove la geodesica è più corta — dove il corpo è più vicino alla curvatura naturale del campo, il percorso di minima resistenza.
La retta geodetica non è una metafora. È letteralmente la struttura matematica che hai codificato nelle equazioni rosse. Chi risolve le equazioni trova i numeri. Chi capisce la geodesica sa perché quei numeri e nessun altro potevano esistere.
Codice:
VS03 = [1, 216, 432, 540, 648, 1620]
VS07 = [12, 24, 36, 48, 60, 232]
VS18 = [1, 12, 24, 36, 48, 90]