Approfondimenti sulle matrici, partendo dalle 8 tabelle di Angela Martini.

[nelson1331]

Ai lettori di Lottoced,
provero' dapprima a fornire una spiegazione (cosi' come mi e' stata trasmessa indirettamente, non avendo partecipato alla realizzazione delle suddette 8 tabelle, da parte di un gruppo di programmatori).
Scopo principale delle medesime, e' quello di creare una sorta di filtro/riduzione molto potente, affinche' dai miei 45 numeri iniziali, possa contrassegnarne pochi con specifici segnali e poi ovviamente giocarli.
Con formazioni da 45 numeri e' facilissimo, in 18 colpi di gioco, conseguire quaterne a volonta' ed in taluni casi anche le cinquine, sulla ruota di calcolo e gioco.
La domanda pero' piu' difficile alla quale dare una risposta, e' questa : quali dei 45 numeri scegliere ? Come faccio a ridurli ?
Ebbene le suddette tabelle sono state studiate allo scopo e benche' non ne conosca tutto l' iter della realizzazione, posso dire che sono strutturate con un buon modello matematico.
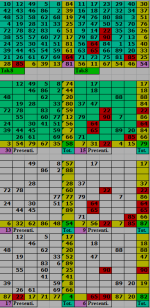
Se io riscontro ad esempio che in una determinata estrazione escano ambi presenti nella tabella in posizioni isotope fra sx e dx e' assai probabile che anche gli altri numeri che si trovano sulle stesse righe e/o colonne, dovranno uscire.

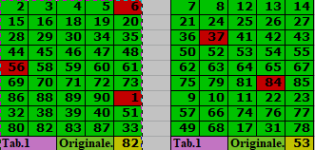
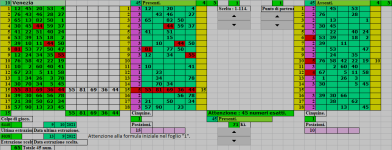
Rispetto alla tabella in allegato, se io leggessi l' ambo 2.7 (1° casella in alto a sx della 1° tabella e 1° casella in alto a dx della 2° tabella), i numeri a seguire (3.4.5.6 e 8.12.13.14 in orizzontale) cosi' come in verticale i numeri (15.28.44.56.69.86.32.80 e 21.36.50.62.75.9.57.49) rappresenterebbero una sequenza ideale per i numeri che sono gia' sortiti.
Pero' le tabelle con la lettura isotopa, presentano diversi problemi o mancanze.
1°) Se io avessi tutti e 5 i numeri nella tabella di sx. come potrei trovare l' isotopia con la tabella di dx. giacche' in essa non vi sarebbe nessun numero ? Impossibile !
2°) Inoltre queste 8 tabelle hanno solo 8 coppie dei parziali totali di tabella, totali che assommati mi devono dare 45.
Dove sono le altre tabelle mancanti e come ricavarle ?
Le coppie con totale= 45 sono : 1.44 2.43 3.42 .... 45.90
3°) Queste 8 tabelle, se le leggiamo esclusivamente in modo isotopo, al fine di ricavare tutti i 4005 ambi, non possono fornirmi tutti gli ambi interessati. Molte di queste combinazioni, sono per cosi' dire, escluse.
Percio' studiando queste tabelle, mi sono chiesto : e' possibile replicarle ma, con la creazione di tutte le 45 tabelle che generano i totali parziali di cui sopra (1.44 2.43 3.44 ....45.90) ?
Per fare questo, ho bisogno di formule matematiche che mi spostino il contenuto della 1° tabella a sinistra e corrispondentemente e non necessariamente, mi cambino le posizioni nella tabella di destra.
Alla fine quale risultato otterro' ?
La tabella di sinistra avra' sempre e solo gli stessi 45 numeri, cosi' come la tabella di destra, avra' sempre e solo gli stessi numeri.
Cosa pero' importante : avranno cambiato le posizioni.
Con questo procedimento o passaggio, posso andare avanti, fino all' infinito.
Si' ho usato proprio il termine giusto : all' infinito.
Perche' usando le formule matematiche, posso modificare le posizioni della 1°tabella, cosi' sempre tramite le medesime formule, posso modificare le medesime posizioni della tabella di destra.
A cosa puo' servire questo lavoro ?
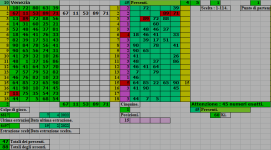
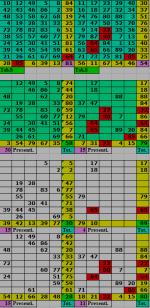
A creare, con le nuove posizioni gli assetti della matrice 5x9 di sinistra e destra e soprattutto per trovare le identita' dei totali di riga e colonna, in entrambe le tabelle.
Poiche' la forza che le muovera' (ossia le formule matematiche), sono sempre le stesse e costanti in entrambi i casi, se verifichero' la condizione isotopa (ma questa volta nei totali di riga o colonna), vorra' dire che vi e' equilibrio e che le 2 formazioni sono accettabili dal punto di vista del gioco.
A voi percio' chiedo : come fareste, con formule matematiche, una volta che abbiate determinato il quadro dei 45 numeri di sinistra a generare con un ordine consequenziale anche la tabella di destra ed andare avanti, all' infinito ?
Se non trovo le condizioni di equilibrio (fra i 45 numeri di sinistra ed i 45 numeri di destra, con i loro totali di riga e colonna) al 1° passaggio, allora proseguo con un ulteriore step : ripetero' i calcoli perche', facendo in questo modo, posso andare avanti all' infinito, fino a quando non riscontro la condizione di equilibrio isotopo, fra i totali delle 2 tabelle.
Luigi B. (anni fa) mi disse che se gli avessi fornito tutto l' iter, sarebbe stato disponibile a trasformare l' idea in un programma.
Posso dirgli che sono in grado di trasmettergli tutte le informazioni necessarie e che se vorra' potra' dare l' ok ed io iniziero' a dire come procedere.
Devo attendere i suoi tempi, poiche' e' impegnato assieme ad Edoardo in un nuovo ed avvincente lavoro.
Percio' Luigi, in questa pagina apro uno spazio per conoscere il parere di altri esperti ma, fondamentalmente per la realizzazione, attendo il tuo ok.
Grazie.

 

[Nikor]

Ciao nelson, non conosco nulla delle matrici che hai menzionato ma se è ancora lecito e possibile esprimere un personale parere scrivo come la penso:
La speranza è di non scatenare un putiferio con i pseudi scienziati , bastian contrari, matematici e sapientoni dell’ultima ora!
Scrivo per quel poco che mi concerne e che ricordo di quando ero studente sul Calcolo Combinatorio che non è altro che una branca della matematica!
Come hai scritto tu all’infinito si può arrivare solo in alcune particolari condizioni ( una la più banale ) che dopo avendo costruito la matrice [ integrale ] la si voglia modificare con particolari posizioni !

Se invece volessimo costruire una matrice Standard che coinvolga tutti i 90 numeri prendendo gruppi di 2 matrici come nel caso che hai usato come esempio la matematica mette un limite ben definito e con l’ausilio del calcolo combinatorio estrapola le formazioni integrali.

Concludo e scrivo ( con la speranza di non aver commesso errori ) le matrici integrali sono
( 1.492.695.054.081 ) che equivalgono ad un bilione & 492 miliardi di formazioni dove splittandole in gruppi ( come quello che hai menzionato come esempio ) diventano la bellezza di ( 165.855.006.009 ) MATRICI !

Di più non so e non avrei neanche la minima idea se un algoritmo possa fungere , sicuramente non sul mio PC.

Spero che intervenga qualcuno più ferrato del sottoscritto perchè in tutta franchezza non so e non avrei la minima idea di come risolvere il problema con questa mole di dati!

Buona settimana, da Nikor.

 

[nelson1331]

Ok Nikor.
Grazie per il tuo intervento : e' proprio questo uno dei motivi, per il quale ho aperto questo post.
Il fulcro dell' argomento, non e' tanto la ripetitivita' dell' algoritmo di calcolo (posso garantirti cio' che ho scritto : cioe' posso movimentare i numeri fino all' infinito) e se Luigi B. potra' intervenire, lo dimostrero'.
L' elemento che invece vorro' evidenziare e' che modificando le posizioni dei 45 numeri, fra la tabella di sinistra e quella di destra, nei loro totali di riga e colonna succedono cose molto interessanti.
Spero vi sia un seguito, con l' aiuto di Luigi B. per dimostrare quanto sopra.
Non e' richiesto il calcolo all' infinito : creo 1 riga da 45 numeri da una parte e 45 numeri dall' altra e poi chiedo la verifica dei totali.
Non trovo la condizione ideale ?
Nessuna problema : proseguo nella creazione di un' altra riga da 45 numeri con diverse posizioni, sia per la tabella di sx che quella di dx.
Dal punto di vista osservativo, posso dirti che creando un quadro di 90 linee (cioe' 90 ripetizioni) per 45 numeri, si delineano con molta accuratezza, i movimenti dei numeri in verticale. Successivamente, postero' alcune immagini, poiche' queste valgono piu' di 1000 parole.

 

[Nikor]

Sei stato chiarissimo, teniamo anche sempre ben presente che nella prima sezione di 9 righe per 5 colonne l'insieme forma ( 1.221.759 gruppi integrali ) cambiando le posizioni bisogna scomodare le ( Permutazioni ) che per ogni riga saranno 120! e per i 45 numeri saranno ben ( 146.611.080 ) !!!
Ciao.

 

[nelson1331]

Eccovi 3 immagini.
Nella 1° immagine la riga con indice=0 e' quella iniziale, cioe' sono i 45 numeri che seleziono a vario titolo (da matematica sommativa, dai numeri spia, dai ritardatari...). Quello che piu' vi piace.
E' una riga importante ma, non e' quella fondamentale per i calcoli.
Una volta letta la riga=0, con gli algoritmi che sono e dovranno essere sempre gli stessi nell' arco dei miei passaggi, posso movimentare le formazioni (tabella di sinistra e destra, che per mia comodita' ho chiamato presenti ed assenti).
Nelle immagini 2 e 3 invece, c' e' il prospetto dell' evoluzione dei 45 numeri (perche' questi sono e saranno sempre quelli iniziali) ma, con posizioni modificate.
La nostra attenzione ora va posta sulla verticale, non potendo fare alcun confronto in orizzontale, poiche' sono sempre gli stessi numeri.
Si delineano percio' delle tracce significative, di numeri che in verticale, andranno a ripetersi, esattamente nella stessa colonna ed uno dietro l' altro.
Questo e' il 1° importante elemento dall' angolo visivo dell' osservatore.
Il 2° e per me ancora piu' importante elemento, e' quando andro' ad incasellare la formazione dei 45 numeri nella sua matrice 5x9 e da questa ricavo i suoi totali di riga e colonna e li confronto con i totali della nuova tabella di destra che definisco degli assenti (che in questa circostanza non ho fotografato).
Solo quando incontrero' valori isotopi dei totali della tabella di sx con quella di dx (minimo almeno 2 valori esattamente identici), potro' pensare che la matrice che si e' creata sia in perfetto equilibrio fra le forze (i medesimi algoritmi, che hanno generato sx e dx).
Posso dirlo con tutta sincerita', che talune circostanze mi hanno permesso di notare in questa configurazione, nelle 5 colonne contenenti i numeri estese a 9 righe, una di esse contiene o il terno o la quaterna (dipende dal punteggio della linea zero) all' interno di una novina e che uscira' su ruota (nei miei test ho ipotizzato fino a 18 concorsi).

 

[nelson1331]

Vi mostrero' un esempio, certamente significativo, per farvi comprendere cosa avviene nello spostamento dei numeri, lungo l' asse verticale (Il piu' importante, poiche' in orizzontale avro' sempre e solo la presenza dei miei 45 numeri iniziali).
L' esempio che andro' ad analizzare e' la cinquina che e' uscita al 12° colpo.
Se io a monte dispongo di una linea, contenente una cinquina che uscira' nell' arco dei 18 concorsi, poiche' sviluppo 90 linee, andro' a generare 450 volte le ripetizioni dei medesimi 5 numeri : giusto ?
Bene, se tutto fosse identico, allora anche nelle colonne, sviluppate nelle formazioni da 45 elementi, dovrei ritrovare : 450/45=10 numeri con ripetizione a vario titolo dei futuri estraendi : giusto ?
Vorrebbe dire, che ogni colonna dovrebbe contenere i 5 numeri (futuri estratti), ripetuti 2 volte : giusto ?
Per la legge dei grandi numeri, pero' quanto suesposto e' solo teorico.
Cosa succede realmente all' interno di ogni colonna ?
Lo leggerete alla linea 120.
Alcune colonne avranno una ripetizione dei futuri estratti ad un determinato colpo di gioco, che si attesta a 7 numeri.
Altre colonne avranno punteggi ben piu' alti arrivando in diversi casi da me analizzati, anche 20-22 ripetizioni.
Globalmente 1 colonna conserva circa 50 ripetizioni totali, dei 45 numeri della linea di partenza : linea 28.
Se notate la colonna 10 ha 16 ripetizioni relative al concorso vincente al 12° colpo.
La colonna 32, ha 15 numeri.
La colonna 40, ha 18 numeri.
Come faccio pero' ad individuare la colonna giusta o semmai 2 o 3 colonne esatte, che mi porterebbero certamente al giocabile ?
Inoltre quando ho iniziato gli studi di questa materia, che nel gergo informatico si chiama "flip-flop" ovvero gli scambi di posizione fra i 45 presenti ed i 45 assenti, mi sono chiesto se poi questi ordinamenti, sarebbero stati veri cosi' come decantati da Angela Martini o da Redmoon.
Se voi vedrete, in questo scenario, che non e' l' eccezione ma, che rientra a buon titolo nella caratteristica insita nella conformazione dei numeri che vengono pilotati ad ogni passaggio in diverse posizioni, cio' che i precedenti autori affermavano e' perfettamente riscontrabile.
Gli ordinamenti per colonna (se fatti bene), vanno a compattare i futuri estraendi.
In questo caso, sulla linea 9 ne trovate ben 4 (ordinati e consecutivi) ed utilizzando l' indice di riga, (posizione 35), vi ritrovate la cinquina.
Il mio suggerimento ed anche le mie domande rivolte a voi, sono queste :
1°) Questo studio, vi sembra utile ?
2°) Le formazioni lette per colonne, possono risultare di grande beneficio per il giocatore ?
3°) Quali sono secondo voi le caratteristiche per selezionare una colonna, anziche' un' altra ?
4°) Infine, (cosa non di 2° piano), come fareste voi, a permutare illimitatamente, sia i 45 numeri dei presenti che i 45 numeri degli assenti ?
Forza e coraggio : attendo i vostri commenti.
Grazie.

 

[lotto_tom75]

Vi mostrero' un esempio, certamente significativo, per farvi comprendere cosa avviene nello spostamento dei numeri, lungo l' asse verticale (Il piu' importante, poiche' in orizzontale avro' sempre e solo la presenza dei miei 45 numeri iniziali).
L' esempio che andro' ad analizzare e' la cinquina che e' uscita al 12° colpo.
Se io a monte dispongo di una linea, contenente una cinquina che uscira' nell' arco dei 18 concorsi, poiche' sviluppo 90 linee, andro' a generare 450 volte le ripetizioni dei medesimi 5 numeri : giusto ?
Bene, se tutto fosse identico, allora anche nelle colonne, sviluppate nelle formazioni da 45 elementi, dovrei ritrovare : 450/45=10 numeri con ripetizione a vario titolo dei futuri estraendi : giusto ?
Vorrebbe dire, che ogni colonna dovrebbe contenere i 5 numeri (futuri estratti), ripetuti 2 volte : giusto ?
Per la legge dei grandi numeri, pero' quanto suesposto e' solo teorico.
Cosa succede realmente all' interno di ogni colonna ?
Lo leggerete alla linea 120.
Alcune colonne avranno una ripetizione dei futuri estratti ad un determinato colpo di gioco, che si attesta a 7 numeri.Vedi l'allegato 2226617Vedi l'allegato 2226618Vedi l'allegato 2226619Vedi l'allegato 2226620
Altre colonne avranno punteggi ben piu' alti arrivando in diversi casi da me analizzati, anche 20-22 ripetizioni.
Globalmente 1 colonna conserva circa 50 ripetizioni totali, dei 45 numeri della linea di partenza : linea 28.
Se notate la colonna 10 ha 16 ripetizioni relative al concorso vincente al 12° colpo.
La colonna 32, ha 15 numeri.
La colonna 40, ha 18 numeri.
Come faccio pero' ad individuare la colonna giusta o semmai 2 o 3 colonne esatte, che mi porterebbero certamente al giocabile ?
Inoltre quando ho iniziato gli studi di questa materia, che nel gergo informatico si chiama "flip-flop" ovvero gli scambi di posizione fra i 45 presenti ed i 45 assenti, mi sono chiesto se poi questi ordinamenti, sarebbero stati veri cosi' come decantati da Angela Martini o da Redmoon.
Se voi vedrete, in questo scenario, che non e' l' eccezione ma, che rientra a buon titolo nella caratteristica insita nella conformazione dei numeri che vengono pilotati ad ogni passaggio in diverse posizioni, cio' che i precedenti autori affermavano e' perfettamente riscontrabile.
Gli ordinamenti per colonna (se fatti bene), vanno a compattare i futuri estraendi.
In questo caso, sulla linea 9 ne trovate ben 4 (ordinati e consecutivi) ed utilizzando l' indice di riga, (posizione 35), vi ritrovate la cinquina.
Il mio suggerimento ed anche le mie domande rivolte a voi, sono queste :
1°) Questo studio, vi sembra utile ?
2°) Le formazioni lette per colonne, possono risultare di grande beneficio per il giocatore ?
3°) Quali sono secondo voi le caratteristiche per selezionare una colonna, anziche' un' altra ?
4°) Infine, (cosa non di 2° piano), come fareste voi, a permutare illimitatamente, sia i 45 numeri dei presenti che i 45 numeri degli assenti ?
Forza e coraggio : attendo i vostri commenti.
Grazie.

Ciao nelson, l'argomento delle matrici numeriche riduzionali mi ha sempre suscitato molto interesse anche se purtroppo anche nel caso dello sviluppo condotto in passato da mirapep e da luigi con tanto di apposito super power programma ad esse dedicato non ci ho mai capito molto... Io ho provato a creare appositi script sperimentali per provare a generarle in modo random della classe voluta (es. 60) e a filtrarne i collimanti su tutti i livelli... ma per adesso questo tipo di analisi non mi ha portato nessun risultato particolarmente interessante... Io quello che che credo di aver capito dal tuo riassunto per ora, e correggimi se sbaglio, è che tu disponi 90 righe di 45 elementi. Ciascuna riga ha gli stessi numeri ma questi elementi che la compongono sono per ogni riga in posizioni diverse (non ho capito che criterio usi per scegliere le posizioni e se questo tipo di scelta è di tipo random o meno). Non mi è chiaro nemmeno nè cosa cerchi all'interno delle 45 colonne... per ridurre la massa numerica iniziale da 45 ad una lunghetta di massimo 20 elementi, nè come scegli la prima riga dei 45 elementi da cui poi discende tutto il resto... Grazie se vorrai esplicitare in modo ancora più esteso il tuo interessante approccio riduzionale con la matrice in oggetto.

 

[nelson1331]

Ciao Lotto_Tom75,
la scelta dei 45 numeri o 1° riga o linea iniziale, di per se', risulta ininfluente.
Puoi scegliere i 45 numeri, fra i superfrequenti, o nella matematica sommativa, o nei numeri spia, o nei ritardatari o altri modi ed anche alla luce dei risultati cambia davvero poco.
La cosa invece importante e' l' algoritmo che determina gli spostamenti delle posizioni.
Questo algoritmo, deve essere lo stesso, sia per i 45 numeri presenti, sia per i 45 assenti.
Percio' non puo' essere random o causale, perche' in tal caso determinerebbe dei cambiamenti da una parte in un certo modo, mentre altererebbe la forma dall' altra parte, ignorando i movimenti che sono occorsi ai primi.
Il modello con algoritmo, ti permette inoltre di controllare i cambiamenti, perche' sai esattamente i punti o le posizioni che andrai a toccare : il metodo random, non ti consente questo approccio, perche' una volta li movimentera' ad esempio di 2 caselle, mentre in un' altra circostanza li spostera' di 15 caselle.
Percio' il modello random e' impossibile da gestire !
Che algoritmo uso ?
Qui dovrai/dovrete dare spazio alle forme mentali di riduzione.
Io uso esclusivamente 2 tipi di calcolo : le somme e le sottrazioni.
Quindi sono operazioni facilissime, che chiunque puo' utilizzare.
Le operazioni di calcolo le faccio sempre partire costantemente dal 1° numero a sx della stringa da 45 numeri.
Adesso lascio a voi l' inventiva, la creativita', la genialita' per dirmi : come procedereste ?
Ogni volta che creo questo quadro 45x90, si determineranno invariabilmente delle mutazioni anche nelle sequenze verticali delle colonne.
Come faccio ad individuare la colonna/colonne (poche max 2-3) ?
1°) Faccio sempre il raffronto con la linea iniziale o linea zero o linea di partenza (i 45 numeri che ho selezionato) per vedere quanti e quali siano i numeri ripetuti (generalmente siamo vicini ai 50 numeri).
2°) Compongo una linea equivalente alla colonna che sto testando, la pongo accanto ma, anziche' partire dal 1° numero parto dal 2° e poi nella 90° posizione andro' ad inserire il 1° elemento di suddetta colonna.
Creo cosi' la tabella degli ambi e dovro' accuratamente verificare, quali siano i ripetuti, poiche' se la sequenza e' giusta, questi ambi ripetuti, benche' in forma diversa creeranno la migliore colonna, quando avranno i totali uguali.
Ho dato qualche spunto in piu' per riflettere ed andare avanti.

 

[lotto_tom75]

Ciao Lotto_Tom75,
la scelta dei 45 numeri o 1° riga o linea iniziale, di per se', risulta ininfluente.
Puoi scegliere i 45 numeri, fra i superfrequenti, o nella matematica sommativa, o nei numeri spia, o nei ritardatari o altri modi ed anche alla luce dei risultati cambia davvero poco.
La cosa invece importante e' l' algoritmo che determina gli spostamenti delle posizioni.
Questo algoritmo, deve essere lo stesso, sia per i 45 numeri presenti, sia per i 45 assenti.
Percio' non puo' essere random o causale, perche' in tal caso determinerebbe dei cambiamenti da una parte in un certo modo, mentre altererebbe la forma dall' altra parte, ignorando i movimenti che sono occorsi ai primi.
Il modello con algoritmo, ti permette inoltre di controllare i cambiamenti, perche' sai esattamente i punti o le posizioni che andrai a toccare : il metodo random, non ti consente questo approccio, perche' una volta li movimentera' ad esempio di 2 caselle, mentre in un' altra circostanza li spostera' di 15 caselle.
Percio' il modello random e' impossibile da gestire !
Che algoritmo uso ?
Qui dovrai/dovrete dare spazio alle forme mentali di riduzione.
Io uso esclusivamente 2 tipi di calcolo : le somme e le sottrazioni.
Quindi sono operazioni facilissime, che chiunque puo' utilizzare.
Le operazioni di calcolo le faccio sempre partire costantemente dal 1° numero a sx della stringa da 45 numeri.
Adesso lascio a voi l' inventiva, la creativita', la genialita' per dirmi : come procedereste ?
Ogni volta che creo questo quadro 45x90, si determineranno invariabilmente delle mutazioni anche nelle sequenze verticali delle colonne.
Come faccio ad individuare la colonna/colonne (poche max 2-3) ?
1°) Faccio sempre il raffronto con la linea iniziale o linea zero o linea di partenza (i 45 numeri che ho selezionato) per vedere quanti e quali siano i numeri ripetuti (generalmente siamo vicini ai 50 numeri).
2°) Compongo una linea equivalente alla colonna che sto testando, la pongo accanto ma, anziche' partire dal 1° numero parto dal 2° e poi nella 90° posizione andro' ad inserire il 1° elemento di suddetta colonna.
Creo cosi' la tabella degli ambi e dovro' accuratamente verificare, quali siano i ripetuti, poiche' se la sequenza e' giusta, questi ambi ripetuti, benche' in forma diversa creeranno la migliore colonna, quando avranno i totali uguali.
Ho dato qualche spunto in piu' per riflettere ed andare avanti.

Ciao nelson, grazie per le ulteriori info ma per adesso purtroppo di nuovo ho capito solo che le posizioni non sono casuali. Temo che se non deciderai di fare esempi più semplici io e molti altri troveremo difficoltà serie nel capire e nel contribuire eventualmente con nuove idee e/o script e/o risposte... riguardanti questo tuo comunque molto interessante tema riduzionale.

Ad ogni modo per quanto riguarda l'algoritmo di scelta posizionale... io avrei pensato ad un semplice slittamento di una posizione da sx verso dx per 45 volte o per 90 volte se questo è il numero di righe necessario per questo tipo di ricerca riduzionale... Ovviamente mi riferisco allo slittamento della 45ina iniziale di base scelta da ognuno secondo le proprie preferenze. Che ne pensi?

 

[lotto_tom75]

Ciao nelson, grazie per le ulteriori info ma per adesso purtroppo di nuovo ho capito solo che le posizioni non sono casuali. Temo che se non deciderai di fare esempi più semplici io e molti altri troveremo difficoltà serie nel capire e nel contribuire eventualmente con nuove idee e/o script e/o risposte... riguardanti questo tuo comunque molto interessante tema riduzionale.

Ad ogni modo per quanto riguarda l'algoritmo di scelta posizionale... io avrei pensato ad un semplice slittamento di una posizione da sx verso dx per 45 volte o per 90 volte se questo è il numero di righe necessario per questo tipo di ricerca riduzionale... Ovviamente mi riferisco allo slittamento della 45ina iniziale di base scelta da ognuno secondo le proprie preferenze. Che ne pensi?

Ecco un esempio visivo dello "slittamento" riguardo la prima riga di base a step 1 da sx a dx che pensavo... In questo esempio i 45 elementi della prima riga sono semplicemente i primi 45 consecutivi... ma ovviamente questi potranno essere sostituiti con quelli risultanti in tutte le prime righe scelte di volta in volta...

 

[mirapep]

Ciao, io non ho compreso una beata mazza, ovviamente mio limite. Come ho già evidenziato in altre discussioni, ogni tanto ricicciano Martini & company. La materia naturalmente affascina perchè cerca di dare alla casualità delle estrazioni un "modello" che nel tempo si dovrebbe ripetere con una certa costanza non nei numeri che vengono sorteggiati ma nelle posizioni che andrebbero ad occupare nelle varie matrici.
Mia opinione, per quello che può contare, è che per stuzzicare la fantasia di programmatori e cervelloni matematici occorre partire da 0 non dando per scontato passaggi che per l'autore risultano elementari dopo anni di applicazione ma per chi legge risultano ripeto di difficile comprensione

 

[vecchione]

Vi mostrero' un esempio, certamente significativo, per farvi comprendere cosa avviene nello spostamento dei numeri, lungo l' asse verticale (Il piu' importante, poiche' in orizzontale avro' sempre e solo la presenza dei miei 45 numeri iniziali).
L' esempio che andro' ad analizzare e' la cinquina che e' uscita al 12° colpo.
Se io a monte dispongo di una linea, contenente una cinquina che uscira' nell' arco dei 18 concorsi, poiche' sviluppo 90 linee, andro' a generare 450 volte le ripetizioni dei medesimi 5 numeri : giusto ?
Bene, se tutto fosse identico, allora anche nelle colonne, sviluppate nelle formazioni da 45 elementi, dovrei ritrovare : 450/45=10 numeri con ripetizione a vario titolo dei futuri estraendi : giusto ?
Vorrebbe dire, che ogni colonna dovrebbe contenere i 5 numeri (futuri estratti), ripetuti 2 volte : giusto ?
Per la legge dei grandi numeri, pero' quanto suesposto e' solo teorico.
Cosa succede realmente all' interno di ogni colonna ?
Lo leggerete alla linea 120.
Alcune colonne avranno una ripetizione dei futuri estratti ad un determinato colpo di gioco, che si attesta a 7 numeri.Vedi l'allegato 2226617Vedi l'allegato 2226618Vedi l'allegato 2226619Vedi l'allegato 2226620
Altre colonne avranno punteggi ben piu' alti arrivando in diversi casi da me analizzati, anche 20-22 ripetizioni.
Globalmente 1 colonna conserva circa 50 ripetizioni totali, dei 45 numeri della linea di partenza : linea 28.
Se notate la colonna 10 ha 16 ripetizioni relative al concorso vincente al 12° colpo.
La colonna 32, ha 15 numeri.
La colonna 40, ha 18 numeri.
Come faccio pero' ad individuare la colonna giusta o semmai 2 o 3 colonne esatte, che mi porterebbero certamente al giocabile ?
Inoltre quando ho iniziato gli studi di questa materia, che nel gergo informatico si chiama "flip-flop" ovvero gli scambi di posizione fra i 45 presenti ed i 45 assenti, mi sono chiesto se poi questi ordinamenti, sarebbero stati veri cosi' come decantati da Angela Martini o da Redmoon.
Se voi vedrete, in questo scenario, che non e' l' eccezione ma, che rientra a buon titolo nella caratteristica insita nella conformazione dei numeri che vengono pilotati ad ogni passaggio in diverse posizioni, cio' che i precedenti autori affermavano e' perfettamente riscontrabile.
Gli ordinamenti per colonna (se fatti bene), vanno a compattare i futuri estraendi.
In questo caso, sulla linea 9 ne trovate ben 4 (ordinati e consecutivi) ed utilizzando l' indice di riga, (posizione 35), vi ritrovate la cinquina.
Il mio suggerimento ed anche le mie domande rivolte a voi, sono queste :
1°) Questo studio, vi sembra utile ?
2°) Le formazioni lette per colonne, possono risultare di grande beneficio per il giocatore ?
3°) Quali sono secondo voi le caratteristiche per selezionare una colonna, anziche' un' altra ?
4°) Infine, (cosa non di 2° piano), come fareste voi, a permutare illimitatamente, sia i 45 numeri dei presenti che i 45 numeri degli assenti ?
Forza e coraggio : attendo i vostri commenti.
Grazie.

ciao Nelson i miei complimenti le tue 12 ore al giorno di lavoro a breve daranno il loro corrispettivo compenso ciao

 

[Lilletto]

Mah
da quello che ho capito la vedo molto difficile che sta cosa funzioni anche perche la Martini non usa le matrici in questo modo.

 

[nelson1331]

Vi propongo questa ricerca, fatta con le 9 tabelle di Angela Martini, attraverso 4 immagini. Siccome molti hanno disprezzato i suddetti lavori, e' bene che possa spezzare una lancia a favore di chi invece, ritiene che attraverso le matrici, si possano ottenere buoni risultati nel gioco del lotto. A differenza di quanto visto fino ad ora, noterete che la lettura ed il confronto fra i 45 numeri e le rispettive tabelle, e' una cosa facile e consueta. Vedrete pero' che ho fatto qualcosa, che fino ad ora non avevo mai visto su Lottoced : la lettura ed il confronto precedente, l' ho replicato un' altra volta, in un modo particolare, nel quale i 2 quadri sottostanti che vengono a generarsi, producono una condizione matematica di tutto rispetto. Avrei cioe' avuto, con le letture abituali, 1 quadro con 15 numeri, contenente la quaterna al 15° colpo. Pero' ho voluto effettuare un' ulteriore filtro/riduzione, per restringere ancora di piu' i numeri, (portandoli rispettivamente a 9 numeri ed a 11) ma, soprattutto perche' vi fosse maggiore sostegno matematico. Come ho fatto secondo voi ? Perche' la tabella 8 (avendo sempre confrontato la medesima ma, con 2 modalita' diverse), ha caratteristiche matematiche speciali ?

 

[claudio8]

Nelson, se facessi un riassunto sarebbe più semplice seguirti.
grazie

 

[Lilletto]

Ciao Nelson
se ti riferisci a Me .... io non disprezzo quello che scrivi anzi almeno ce' qualcuno che tenta di fare qualcosa.
La mia critica se cosi si puo' dire e' riferita alle tabelle della Martini che probabilmente le ha create Lei e solo Lei sa come usarle, quello che stai facendo Tu e' una Tua interpretazione che purtroppo non ti porta da nessuna parte, spero che non te la prenda perche' non e' mia intenzione di offenderti e magari puo' essere che mi sbaglio.
Buon Lavoro.

 

[nelson1331]

La 1° parte del lavoro e' facile. E' sufficiente fare il controllo dei 45 numeri individuati e poi domandarsi, in corrispondenza a ciascuna tabella e relativa casella : il numero dei 45 e' presente nella tabella, oppure no ? Se e' presente, riscrivo la tabella con la stessa sagoma ma, questa volta riportero' solo i numeri che sono uguali ai 45 da me selezionati. Percio' alla fine, facendo il riscontro fra tabella di sx e quella di destra, dovro' sempre trovare 45 caselle impegnate e 45 caselle vuote o bianche. Il difficile diventa il 2° passaggio, che mi servira' per ridurre ancora di piu' la massa numerica, mantenendo inalterati i punti acquisiti, corroborarando con calcoli matematici, perche' alcuni quadri avranno possibilita' di vincite piu'alte, mentre per altri non sara' cosi'. Per darvi un aiuto, posso solo dirvi, che il 2° passaggio e' dettato dalle posizioni. In questo modo, anziche' avere solo 2 quadri, posso disporne di 4 e fare le appropriate verifiche di quadratura, fra i totali di colonna e riga, sia verticali, orizzontali e diagonali. Prendete carta, penna e calcolatrice e vedrete che vi sono quadrature perfette.

 

[Lilletto]

Be allora diciamo che funziona
Secondo Te Nelson che tipo di vincite riesci ad ottenere?
e in quali tempi di attesa?
Riesci a ottenere un buoni risultato ad ogni previsione oppure alcune fanno cilecca?
Ti spiego la mia perplessita che mi rimane difficile credere che puoi ottenere delle vincite di terno e quaterna con i totali di righe e colonne.
Scusa la mia franchezza.

 

[Lilletto]

Ok .... grazie Nelson della risposta al limite dacci una dimostrazione con una previsione

 

[Lilletto]

Ciao Nelson1331 ..... ma poi queste tabelle della Martini sei riuscito a farle funzionare?