How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Nota: This feature may not be available in some browsers.
Stai usando un browser molto obsoleto. Puoi incorrere in problemi di visualizzazione di questo e altri siti oltre che in problemi di sicurezza. .
Dovresti aggiornarlo oppure usare usarne uno alternativo, moderno e sicuro.
Dovresti aggiornarlo oppure usare usarne uno alternativo, moderno e sicuro.
Ba e Ca e la tecnica obliqua
- Creatore Discussione Zetrix
- Data di inizio
Zetrix
Advanced Premium Member
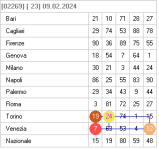
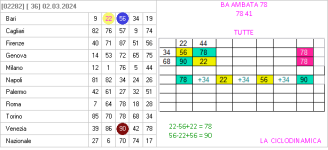
toon provo a spiegarti la tecnica allora si devono rilevare due ambi con la stessa differenza
su ruote consecutive come vedi in tabella ma non basta solo questa condizione
i numeri a e b devono essere minore e maggiore e lo stesso vale per gli altri due numeri..
in pratica devi fare questa prova 19+5=24 e 7+5=12 ..condizione valida..
se invece ai 24 19 questa condizione non e valida..
inoltre se ai notato nella tabella si deve aggiungere un altra condizione e che due numeri devono essere isotopi
fatto questo si mette in gioco i due numeri rimanenti ma si puo dire anche i due numeri esclusi
che sono il 15 63 e questo ambo gioca su tutte
aggiungo un altra nota se nel caso questo ambo e sortito nella estr di calcolo oppure
nella estrazione indietro di una estrazione la condizione non la si mette in gioco..
Ultima modifica:
Zetrix
Advanced Premium Member
del programma in VB5 so che ce ne era uno nel forum, ma no ricordo dove, non riesci apassarmelo o dirmi dove trovarlo?
La tecnica sembra interessante, per ambata.
toon il programma visual lotto 5 lo trovi in diversi forum forse anche qua..
Zetrix
Advanced Premium Member
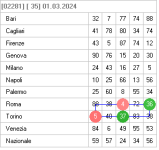
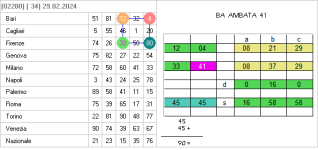
nell'ultima estrazione ce questa condizione a roma e torino ma i due numeri in gioco 88 38
sono usciti a roma nella estrazione di calcolo quindi a dato gia esito..
in alternativa si puo giocare l'ambata 41 la somma di 4+37 ma questa e un altra tecnica..
Numeri in gioco 41 su RO TO per Estratto
Ultima modifica:
Zetrix
Advanced Premium Member
Zetrix
Advanced Premium Member
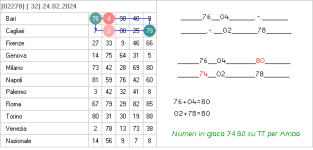
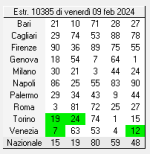
toon non ai visto ancora niente ho altre tecniche potentissime ma non voglio mettere troppe cose nel forum..
ieri ho giocato il 42 78 a bari ma e uscito a venezia..! adesso il 78 a bari a 199 estr di ritardo..
se martedi il 78 non e esce a bari tocca le 200 estr e batte tutti i record..
fai una statistica sulle venus e vedi se qualche numero a superato le 200 estr..
purtroppo non gioco a tutte perche si spende troppo ogni tanto gioco un ambo su tutte..
ieri ho giocato il 42 78 a bari ma e uscito a venezia..! adesso il 78 a bari a 199 estr di ritardo..
se martedi il 78 non e esce a bari tocca le 200 estr e batte tutti i record..
fai una statistica sulle venus e vedi se qualche numero a superato le 200 estr..
purtroppo non gioco a tutte perche si spende troppo ogni tanto gioco un ambo su tutte..
toon non esagerare con i complimenti sono studi come li fanno tanti altri nel settore del lotto..
Ultima modifica:
Missione Impossibile.
Banned
Il 78 lo stò giocando anche io..
Però non ho l'archivio aggiornato di VL5...
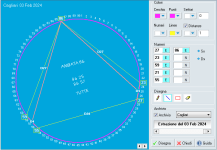
Ma spiega la ciclodinamica in che consiste...
LA CICLODINAMICA
LA CICLODINAMICA. 1^ parte
La pratica fondamentale dello studioso di ciclometria è quella di segnare i numeri lungo la circonferenza e di tracciare le corde di distanza fra i relativi punti. In questo modo, venendosi a configurare dei poligoni inscritti è possibile leggere nel corso delle estrazioni, ovviamente entro uno spazio definito dal calcolo delle probabilità, una serie di geometrie. La “lettura geometrica”, resa possibile dalla numerazione chiusa e ripetitiva dell’insieme dei 90, va decifrata correttamente con l’algebra e l’aritmetica modulare. All’interno del fascicolo “LA CICLOMETRIA. Armonia e Simmetrie nel gioco del Lotto”, supplemento del numero di Totocorriere uscito nel marzo del ‘91, l’autore Domenico Manna, fra diversi argomenti trattati, illustrò le basi della Ciclodinamica, definita nell’occasione come “lo studio del movimento circolare nel tempo dei numeri lungo la circonferenza”.La ciclodinamica in senso orario è positiva e si indica con il segno “+”.
Ad esempio, se consideriamo i numeri 1 e 12, dal numero 1 al numero 12 abbiamo una ciclodinamica positiva di (+11):
1 (+11) è12
Il valore della ciclodinamica, però, non è assoluto, ma relativo al punto di osservazione. Pertanto, la ciclodinamica della coppia suesposta può essere anche letta nel verso opposto, cioè in senso antiorario. In questo caso si registra una ciclodinamica negativa di (–11):12 (-11) è1
Se invece rileviamo una terna di numeri con due ciclodinamiche uguali nel modulo, ma con verso opposto, allora abbiamo due ciclodinamiche simmetriche:80 ç (-11) 1 (+11) è12
Dal numero 1 al numero 12 la ciclodinamica è (+11), mentre dal numero 1 all’80 è (–11): le due ciclodinamiche sono simmetriche. Se gli elementi di cui andremo a stabilire le ciclodinamiche apparterranno alla stessa estrazione si tratterà di una geometrizzazione statica, altrimenti la geometrizzazione sarà dinamica (numeri esaminati estratti in due diverse prove) o parzialmente dinamica (alcuni numeri estratti in concorsi diversi, altri estratti nella stessa prova). Le ciclodinamiche dei 5 numeri di una qualsiasi estrazione sono 20 e si tratta, naturalmente, di una geometrizzazione statica. Ogni numero, che forma quattro ambi con gli altri estratti, ha quattro ciclodinamiche, ognuna di esse simmetrica alla relativa distanza fra gli elementi considerati. Ipotizziamo che i numeri estratti siano i seguenti: 11-63-65-48-89. Il numero 11, per esempio, forma con gli altri estratti 4 ambi. Tra parentesi in 2^ colonna abbiamo le relative distanze (D), mentre a destra abbiamo indicato le ciclodinamiche (CD), simmetriche ad ogni distanza:| 11 | (D= -38) | 63 | (CD= +38) è | 49 |
| 11 | (D= -36) | 65 | (CD= +36) è | 47 |
| 11 | (D=+37) | 48 | (CD= -37) è | 64 |
| 11 | (D= -12) | 89 | (CD= +12) è | 23 |
2a | 2b | 2c | 2d | 2e | |
-a | - | 2b-a | 2c-a | 2d-a | 2e-a |
-b | 2a-b | - | 2c-b | 2d-b | 2e-b |
-c | 2a-c | 2b-c | - | 2d-c | 2e-c |
-d | 2a-d | 2b-d | 2c-d | - | 2e-d |
-e | 2a-e | 2b-e | 2c-e | 2d-e | - |
Compiliamo per esempio il prospetto per la seguente cinquina 12-25-81-11-10.
Sulla linea orizzontale in alto riportiamo i raddoppi dei numeri base:
| 2a = 2 x 12 = 24 |
| 2b = 2 x 25 = 50 |
| 2c = 81 x 2 = 72 |
| 2d = 11 x 2 = 22 |
| 2e = 10 x 2 = 20 |
a = 78 | b = 65 | c = 9 | d = 79 | e = 80 |
2a | 2b | 2c | 2d | 2e |
24 | 50 | 72 | 22 | 20 |
-a | 78 | |||
-b | 65 | |||
-c | 9 | |||
-d | 79 | |||
-e | 80 |
2a | 2b | 2c | 2d | 2e | ||
24 | 50 | 72 | 22 | 20 | ||
-a | 78 | * | 38 | 60 | 10 | 8 |
-b | 65 | 89 | * | 47 | 87 | 85 |
-c | 9 | 33 | 59 | * | 31 | 29 |
-d | 79 | 13 | 39 | 61 | * | 9 |
-e | 80 | 14 | 40 | 62 | 12 | * |
89ç (-13) 12 (13) 25
Lo strumento si dimostra di enorme utilità per l’appassionato che si vuole cimentare in ricerche e applicazioni di una certa importanza. Daremo qualche accenno nella seconda parte.Fabio Ruotolo
LA CICLODINAMICA. 2^ parte
Come anticipato nella prima parte del servizio cerchiamo qualche applicazione pratica.Le “simmetrie” generate all’interno del prospetto, cioè i numeri ricavati con le somme incrociate dei valori esterni, possono costituire delle formazioni in possesso di particolari caratteristiche stabilite a priori, ma evidentemente la formazione base deve soddisfare certe condizioni. Ricerchiamo, per esempio, una terna con queste caratteristiche:
“b” e “c” è due numeri qualsiasi;
a = 3 (b-c) è triplo della distanza fra gli altri due numeri;
Consideriamo la coppia 4-13 estratta sulla ruota di Milano nell’estrazione n° 137 del 2007.
La distanza ciclometrica fra i due numeri è pari a 9. Il numero “a”, da ricercare su un’altra ruota nella stessa estrazione, deve essere pari al triplo della distanza dell’ambo rintracciato:
a = 3 x (b-c) = 3 x 9 = 27
Il numero 27 non è presente su una delle altre nove ruote, pertanto invertiamo la disposizione dei due numeri rilevati:a = 3 x 81 = 63
Il secondo risultato è ovviamente pari al complementare a 90 del primo. Il numero 63 lo troviamo però nel medesimo sorteggio sulla ruota di Cagliari.Assegniamo alla lettera “a” il triplo della distanza e alle lettere “b” e “c” i numeri dell’ambo base in modo da avere la ciclodinamica positiva dalla “c” alla “b” .
a = 63 b = 4 c = 13
Compiliamo il prospetto delle simmetrie dei tre numeri rintracciati:2a | 2b | 2c | ||
36 | 8 | 26 | ||
-a | 27 | - | 35 | 53 |
-b | 86 | 32 | - | 22 |
-c | 77 | 23 | 85 | - |
53 + 32 = 85
Il numero somma 85 esce al 7° colpo sulla ruota di Cagliari.Al 14°, sempre su Cagliari, troviamo il terno 53-22-23.
Senz’alcun dubbio il lettore potrà trovare più interessante un’applicazione sul prospetto per quattro numeri.
Soddisfando una sola condizione saremo in grado, operando con le ciclodinamiche, di risalire a quattro elementi che formano un quadrato ciclometrico.
La condizione è la seguente: la differenza tra il quarto e il secondo numero (d-b) deve essere pari al triplo della differenza tra il primo e il terzo (a-c).
Concorso n° 137/’07, ruote di Napoli e Palermo.
| NAPOLI 30 37 PALERMO 72 3 |
37 – 30 = 7; 3 – 72 = 21; 7 x 3 = 21;
Compiliamo il prospetto riempiendo soltanto le celle fondamentali, vale a dire le proiezioni antiorarie delle distanze fra le coppie consecutive di posto.a = 37; b = 72; c = 30; d = 3;
I numeri ricavati, 2-24-57-59 formano un quadrato ciclometrico con somma comune 26.2a | 2b | 2c | 2d | ||
74 | 54 | 60 | 6 | ||
-a | 53 | - | - | - | 59 |
-b | 18 | 2 | - | - | - |
-c | 60 | - | 24 | - | - |
-d | 87 | - | - | 57 | - |
Dopo appena 5 estrazioni esce l’ambo 2-24 su Napoli, ruota base.
Fabio Ruotolo
Scusate l'intrusioneGrazie molto interessanteLA CICLODINAMICA
LA CICLODINAMICA. 1^ parte
La pratica fondamentale dello studioso di ciclometria è quella di segnare i numeri lungo la circonferenza e di tracciare le corde di distanza fra i relativi punti. In questo modo, venendosi a configurare dei poligoni inscritti è possibile leggere nel corso delle estrazioni, ovviamente entro uno spazio definito dal calcolo delle probabilità, una serie di geometrie. La “lettura geometrica”, resa possibile dalla numerazione chiusa e ripetitiva dell’insieme dei 90, va decifrata correttamente con l’algebra e l’aritmetica modulare. All’interno del fascicolo “LA CICLOMETRIA. Armonia e Simmetrie nel gioco del Lotto”, supplemento del numero di Totocorriere uscito nel marzo del ‘91, l’autore Domenico Manna, fra diversi argomenti trattati, illustrò le basi della Ciclodinamica, definita nell’occasione come “lo studio del movimento circolare nel tempo dei numeri lungo la circonferenza”.
La ciclodinamica in senso orario è positiva e si indica con il segno “+”.
Ad esempio, se consideriamo i numeri 1 e 12, dal numero 1 al numero 12 abbiamo una ciclodinamica positiva di (+11):
1 (+11) è12Il valore della ciclodinamica, però, non è assoluto, ma relativo al punto di osservazione. Pertanto, la ciclodinamica della coppia suesposta può essere anche letta nel verso opposto, cioè in senso antiorario. In questo caso si registra una ciclodinamica negativa di (–11):
12 (-11) è1Se invece rileviamo una terna di numeri con due ciclodinamiche uguali nel modulo, ma con verso opposto, allora abbiamo due ciclodinamiche simmetriche:
80 ç (-11) 1 (+11) è12Dal numero 1 al numero 12 la ciclodinamica è (+11), mentre dal numero 1 all’80 è (–11): le due ciclodinamiche sono simmetriche. Se gli elementi di cui andremo a stabilire le ciclodinamiche apparterranno alla stessa estrazione si tratterà di una geometrizzazione statica, altrimenti la geometrizzazione sarà dinamica (numeri esaminati estratti in due diverse prove) o parzialmente dinamica (alcuni numeri estratti in concorsi diversi, altri estratti nella stessa prova). Le ciclodinamiche dei 5 numeri di una qualsiasi estrazione sono 20 e si tratta, naturalmente, di una geometrizzazione statica. Ogni numero, che forma quattro ambi con gli altri estratti, ha quattro ciclodinamiche, ognuna di esse simmetrica alla relativa distanza fra gli elementi considerati. Ipotizziamo che i numeri estratti siano i seguenti: 11-63-65-48-89. Il numero 11, per esempio, forma con gli altri estratti 4 ambi. Tra parentesi in 2^ colonna abbiamo le relative distanze (D), mentre a destra abbiamo indicato le ciclodinamiche (CD), simmetriche ad ogni distanza:
11 (D= -38) 63 49 11 (D= -36) 65 47 11 (D=+37) 48 64 11 (D= -12) 89 23
Con l’aiuto dell’algebra è possibile compilare un prospetto che riassume le 20 ciclodinamiche fra i 5 estratti: il prospetto delle Simmetrie, uno strumento che consente di calcolare rapidamente, come in una tavola pitagorica, tutte le simmetrie bilaterali fra le coppie di numeri di una qualsiasi formazione.
Sulla linea orizzontale in alto si inseriscono i raddoppi dei numeri base mentre sulla prima colonna a sinistra si riportano i complementari a 90 dei numeri base. Nelle celle interne, sommando i valori esterni come in una tavola pitagorica, avremo le proiezioni dinamiche fra le varie coppie considerate.
Compiliamo per esempio il prospetto per la seguente cinquina 12-25-81-11-10.
Sulla linea orizzontale in alto riportiamo i raddoppi dei numeri base:
2a = 2 x 12 = 24 2b = 2 x 25 = 50 2c = 81 x 2 = 72 2d = 11 x 2 = 22 2e = 10 x 2 = 20
Compiliamo invece la verticale a sinistra con i complementari a 90 dei numeri base:
Ecco il prospetto con le linee esterne complete:
Quindi, inseriamo nelle celle interne le somme incrociate dei valori esterni:
I valori interni non sono altro che i movimenti simmetrici della distanza fra tutte le coppie componibili con gli elementi della formazione considerata. Il numero 89 per esempio, ricavato con l’operazione 2a-b, è la chiusura triangolare della coppia a-b, infatti:
89ç (-13) 12 (13) 25Lo strumento si dimostra di enorme utilità per l’appassionato che si vuole cimentare in ricerche e applicazioni di una certa importanza. Daremo qualche accenno nella seconda parte.
Fabio Ruotolo
LA CICLODINAMICA. 2^ parte
Come anticipato nella prima parte del servizio cerchiamo qualche applicazione pratica.
Le “simmetrie” generate all’interno del prospetto, cioè i numeri ricavati con le somme incrociate dei valori esterni, possono costituire delle formazioni in possesso di particolari caratteristiche stabilite a priori, ma evidentemente la formazione base deve soddisfare certe condizioni. Ricerchiamo, per esempio, una terna con queste caratteristiche:
“b” e “c” è due numeri qualsiasi;
a = 3 (b-c) è triplo della distanza fra gli altri due numeri;
Consideriamo la coppia 4-13 estratta sulla ruota di Milano nell’estrazione n° 137 del 2007.
La distanza ciclometrica fra i due numeri è pari a 9. Il numero “a”, da ricercare su un’altra ruota nella stessa estrazione, deve essere pari al triplo della distanza dell’ambo rintracciato:
a = 3 x (b-c) = 3 x 9 = 27Il numero 27 non è presente su una delle altre nove ruote, pertanto invertiamo la disposizione dei due numeri rilevati:
a = 3 x 81 = 63Il secondo risultato è ovviamente pari al complementare a 90 del primo. Il numero 63 lo troviamo però nel medesimo sorteggio sulla ruota di Cagliari.
Assegniamo alla lettera “a” il triplo della distanza e alle lettere “b” e “c” i numeri dell’ambo base in modo da avere la ciclodinamica positiva dalla “c” alla “b” .
a = 63 b = 4 c = 13Compiliamo il prospetto delle simmetrie dei tre numeri rintracciati:
I numeri che occupano le celle 2c-a, 2a-b e 2b-c, 53-32-85, formano una terzina di somma, detta anche Triade di Fabarri:
53 + 32 = 85Il numero somma 85 esce al 7° colpo sulla ruota di Cagliari.
Al 14°, sempre su Cagliari, troviamo il terno 53-22-23.
Senz’alcun dubbio il lettore potrà trovare più interessante un’applicazione sul prospetto per quattro numeri.
Soddisfando una sola condizione saremo in grado, operando con le ciclodinamiche, di risalire a quattro elementi che formano un quadrato ciclometrico.
La condizione è la seguente: la differenza tra il quarto e il secondo numero (d-b) deve essere pari al triplo della differenza tra il primo e il terzo (a-c).
Concorso n° 137/’07, ruote di Napoli e Palermo.
Le distanze ciclometriche dei due ambi sono una pari al triplo dell’altra.
NAPOLI 30 37
PALERMO 72 3
37 – 30 = 7; 3 – 72 = 21; 7 x 3 = 21;Compiliamo il prospetto riempiendo soltanto le celle fondamentali, vale a dire le proiezioni antiorarie delle distanze fra le coppie consecutive di posto.
a = 37; b = 72; c = 30; d = 3;
I numeri ricavati, 2-24-57-59 formano un quadrato ciclometrico con somma comune 26.
Dopo appena 5 estrazioni esce l’ambo 2-24 su Napoli, ruota base.
Fabio Ruotolo
Scusate l'intrusione
Ultima estrazione Lotto
-
Estrazione del lotto
giovedì 26 febbraio 2026Bari8645225680Cagliari2546601402Firenze8630430362Genova0783576014Milano3926635465Napoli1359181584Palermo8178588782Roma6936513371Torino1954342625Venezia3723054426Nazionale0728896327Estrazione Simbolotto
Cagliari



 3831222939
3831222939