Asuniverso
Advanced Member >PLATINUM PLUS<
"IL QUADRO CHE EMERGE DA TUTTO QUESTO"
Lo sviluppo matematico non è però semplicemente una questione di istruzione codificate. Esse posseggono in effetti un significato solo in un contesto in cui possano essere applicate, nello stesso modo in cui un programma per computer è inutile senza un computer che lo faccia girare. Questo è il massimo problema nei giochi d'azzardo non ancora risolto e nessuno conosce realmente la risposta... Buona lettura.
Varie scuole di pensiero spesso, rispettabili e rispettate, si fondono sul misticismo dei numeri, non che non si possono progettare buoni edifici con questi metodi; il fatto è che il senso della progettazione logica svolge il ruolo notevolmente più importante, mentre la cornice mistica è così flessibile che vi si può incorporare qualsiasi progetto con sistemi che non hanno alcuna somiglianza, o le assomigliano solo in virtù di una totale flessibilità.
Quando ci si trova a dover affrontare una situazione complicata, spesso la cosa migliore è quella di porsi a cercare di risolvere i problemi, giusto per avere un'idea della direzione nella quale si sta andando. La nostra scelta potrà quindi essere guidata soltanto da considerazioni nelle quali la valutazione personale svolga un ruolo essenziale, vi sono, ciò nondimeno, soluzioni che tutti vorranno scartare a causa della difficoltà e altre invece che tutti preferiranno a causa delle loro semplicità.
E’ chiaro comunque che il buon senso non fa difetto nemmeno ai più esperti quando in problemi concreti riconoscono che le informazioni disponibili sono qualitativamente diverse fra loro. La differenza essenziale da rilevare è nell’attribuzione del perché: è il nostro pensiero che deve trovare dei rapporti di casualità per descriverli, coordinarli e renderne possibile la previsione. E questo che consente di formalizzare il procedimento induttivo traducendo in forma matematica e logica il concetto di causa che sta alla base di ogni nostra previsione, di ogni nostra formulazione di regolarità statistica. Ecco perché la teoria delle probabilità, logica dell’incertezza, deve essere considerata come la premessa dell’intero ragionamento induttivo.
Tutti i rapporti spaziali a noi noti sono misurabili, cioè possono essere ricondotti alla determinazione di grandezza. Perciò i problemi della geometria possono essere risolti anche cercando metodi per calcolare grandezze incognite da quelle note. Questo è quello che si fa nella geometria analitica, nella quale tutte le figure dello spazio vengono trattare solo come grandezza e sono determinate da altre grandezze. La linea retta è definita come la più breve fra due punti, ciò che è una determinazione di grandezza.
Si può dunque anche partire da quest’aspetto del concetto di spazio, secondo cui la posizione di ogni punto può essere determinata da misura concernente una qualche figura spaziale considerata fissa (sistema di coordinate), e poi esaminare quali particolari caratteristiche compete al nostro spazio, in termini di misure effettivamente eseguibili, e come lo differenziano da grandezze estese di pari molteplicità. Questa via ha il particolare vantaggio che tutte le operazioni che compaiono in essa sono pure determinazioni di grandezza mediante il calcolo, per cui viene a mancare del tutto il pericolo che dati abituali della percezione sono scambiati per necessità del pensiero.
Il numero delle misure necessarie per dare la posizione di un punto è uguale al numero delle dimensioni dello spazio considerato. In una linea sono sufficienti la distanza da un punto fisso e quindi una sola grandezza; in una superficie si devono dare le distanze di due punti fissi, mentre nello spazio tre punti. Le ipotesi che ho dovuto porre alla base del calcolo sono le seguenti.
In primo luogo, per rendere possibile una trattazione matematica, si deve supporre che la posizione di ogni punto di A rispetto a certe figure spaziali considerate immutabili e fisse possa venire determinata da misure di un qualche genere di grandezze spaziali, siano esse linee o linee fra superfici. Come è noto, le misure necessarie per la determinazione della posizione di un qualsiasi punto A prendono il nome di coordinate del punto. Il numero delle coordinate in generale necessarie per la completa determinazione della posizione di un punto qualsiasi definisce il numero di dimensioni dello spazio in esame. Si suppone inoltre che il moto del punto A le grandezze usate quali coordinate variano con continuità.
In secondo luogo la definizione di corpo numerico ovvero di sistema rigido di punti deve essere data, come e necessario, in modo da permettere il confronto di grandezze spaziali per congruenza. La definizione del corpo numerico può venire data semplicemente dal seguente criterio: fra le coordinate di due punti qualunque appartenenti a un corpo numerico deve sussistere un’equazione, che esprime una relazione spaziale e temporale fra i due punti invariante per qualunque movimento del corpo relazione che risulta infine essere la loro distanza e che è la stessa per coppie di punti congruenti. Si definiscono congruenti coppie di punti tali che possono essere fatte coincidere una dopo l’altra con una medesima coppia di punti fissi nello spazio.
Gli elementi A, B, C d’anno tre distinte coppie di punti: AB, AC, BC
Per illustrare meglio come funziona, considererò una soluzione particolare, che sarà possibile, è vero, solo se le condizioni iniziali della distanza della massa estrattiva non subisca alcuna alterazione con lo scorrere del tempo (incremento massa estrazionale), la distanza deve sempre avere le condizioni iniziali, non deve subire alcuna variazione.
Le coordinate della linea AB sono la distanza rappresenta dai valori 0.00012959997. L’osservatore, perciò, dirà cosa rappresenta quel valore?
Se si definisce la quantità di moto di un corpo di tre elementi (che viaggia come se fosse un corpo unico); dal prodotto della sua massa * la sua velocità otteniamo la misura di forza agente sul corpo stesso.
Valori integrali
Distanza estrazionale =
= massa * velocità =
= 0.00012959997 massa * velocità 1666667 = 216
Di conseguenza l’intervallo spaziale =
= massa * velocità =
= 0.00000719999 massa * velocità 1666667 = 12
Da cui segue l’intervallo temporale =
= massa * velocità =
= 0.00002159999 massa massa * velocità 1666667 = 36
Questi numeri non sono stati scelti per semplicità, 216,12, 36, ma non sono molto lontani dal vero. Quel che dobbiamo fare, perciò, è cominciare a formulare domande molto generali, prescindendo il più possibile da ogni connessione con la fisica reale del moto dei corpi numerici. Questo modo di procedere è contrario alle tendenze tradizionali nella dinamica dei corpi numerici, ma ha un senso matematico e scientifico: capire prima la natura generale del problema, poi usare tale comprensione per progettare un attacco frontale.
Tutto questo presenta il vantaggio di un trasferimento di tecnologia, quanto meno specifici sono i nostri assunti sulla dinamica del moto numerico, tanto più largamente applicabili possono essere i nostri risultati. Ci chiediamo quindi: quali sono le conformità del sistema? Qual è il catalogo dei tipi di comportamento possibili in un sistema che possegga tale conformità?
Che cosa dobbiamo calcolare per determinare quale di tali comportamenti possibili si verifichi realmente, e quale sia la sua stabilità? Solo dopo aver risposto a queste domande generali cominceremo a calcolare i valori che ci interessano. Dobbiamo ammettere che non otterremo tutti i particolari che potremmo conseguire con una simulazione numerica completa: questo è il prezzo che dobbiamo pagare. In compenso, però, otterremmo una vasta comprensione matematica non solo di questo sistema, ma di qualsiasi altro sistema con le stesse conformità.
Quel che stiamo dicendo è che ci sono strategie alternative disponibili a seconda di ciò che si vuole conoscere, e che strategie diverse sono efficaci su tipi diversi di problemi. L’applicazione della matematica alla scienza numerica è un processo continuo in cui noi impariamo quali siano gli strumenti migliori per risolvere qualsiasi problema dato. Le generalità della rottura di conformità forniscono non solo un nuovo strumento, bensì un intero nuovo armamentario di strumenti.
Dobbiamo chiederci da dove vengono queste particolari determinazioni che caratterizzano il concetto generale di grandezza estesa. Quando osserviamo un corpo numerico che agisce a distanza su un altro, prima di decidere se si tratta di un’azione diretta e immediata, generalmente guardiamo se vi è qualche connessione di misura tra i due corpi; e se troviamo un nesso che possa render conto dell’interazione osservata.
E’ dunque evidente che in molti casi l’azione tra corpi numerici distanti può essere spiegata da una sequenza di azioni di ciascun elemento di una serie di corpi numerici occupanti lo spazio interposto sul successivo. Tutte queste idee sono antiche e ben note per i veri cultori di statistica, ma la teoria ha assunto la sua forma definitiva soltanto dopo l’introduzione del teorema Timeline Sequenza Temporale.
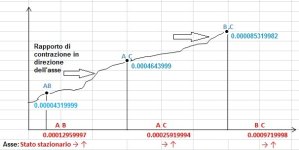
Per illustrare meglio come funziona questa contrazione, considererò una soluzione quella del segmento AB, che sarà possibile, è vero, solo se le condizioni iniziali del moto sono del tutto eccezionali, ma che potrà comunque servirci d’esempio anche per il resto dei segmenti AC, BC.
Segmento AB
Valori integrali
Distanza estrazionale =
= massa * velocità =
= 0.00012959997 massa * velocità 1666667 = 216
Di conseguenza l’intervallo spaziale =
= massa * velocità =
= 0.00000719999 massa * velocità 1666667 = 12
Da cui segue l’intervallo temporale =
= massa * velocità =
= 0.00002159999 massa * velocità 1666667 = 36
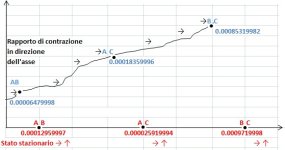
Segmento AB
Valori in contrazione
Distanza estrazionale =
= massa * velocità =
= 0.00004319999 massa * velocità 1666667 = 72
Di conseguenza l’intervallo spaziale =
= massa * velocità =
= 0.00000239999 massa * velocità 1666667 = 4
Da cui segue l’intervallo temporale =
= massa * velocità =
= 0.00000959999 massa * velocità 1666667 = 16
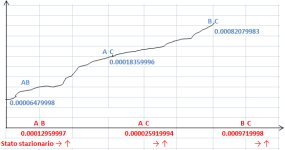
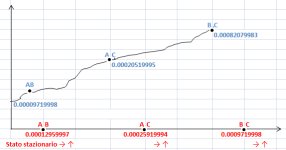
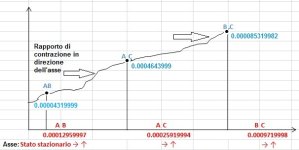
Da queste considerazioni è possibile concludere che il fenomeno che si verifica con lo scorrere del tempo, ossia il fatto che i corpi numerici, la massa estrazionale, gli intervalli spaziali e temporali si contraggono drasticamente su valori integrali, modifica lo spostamento spaziale e temporale.
Lo stato del sistema dipende da tre parametri, di modo che sia possibile rappresentarlo mediante le linee AB, AC, BC . L'insieme delle linee che rappresentano i diversi stati possibili non sarà allora l'intero spazio, ma bensi un numero di regioni disseminati nello spazio. Se assumiamo il determinismo ai primi tre stati , questi debbono essere considerati equiprobabili. Procedendo così, si vede che tutti gli stati che potremmo prima o poi raggiungere non debbono essere considerati equiprobabili, ma come stati possibili in fase di decelerazione AB, AC, BC.
Per quasi un secolo gli studiosi si sono affaticati su questo problema, apportanto grande testimonianza eloquente della rapidità con cui i concetti matematici permeano la cultura umana. E' chiaro a che punto si trovi la questione: ma modificarle è parso necessario. Ovviamente possono esserci altre altre vie, ma che nessuno fino ad oggi a trovato l'idea; quindi preciso, la natura del problema, che in primis portiamo su questa pagine.
E' scontato che con i 90 corpi numerici si vengono a formare 117.480 terne, ma il punto culminante della nostra ricerca e la dimostrazione che dalle ridisposizioni o permutazioni le terne aumentano di numero.
Per esempio, le tre soluzioni a, b, c possono in generale essere permutate in sei modi:
abc, acb, bac, bca, cab, cba, proseguendo su questa strada qualsiasi terna ha le sue sei permutazioni.
Permutazione dellala terna 1-2-3
ridisposizioni: 1-2-3; 1-3-2; 2-1-3; 2-3-1; 3-1-2; 3-2-1
Le permutazioni sono sconosciuti e lontanissime dai cultori di statistica. C'è però un senso molto reale in cui i gruppi di permutazioni possono essere concepite come gruppi di estenzione. Una permutazione è di per sè una trasformazione, non di uno spazio, bensì della collezione di soluzione aggiuntive. E' una ridisposizione, un modo di prenderle e risistemarle.
Si arriva così ad ottenere, dalla terna originaria, le loro 6 permutazioni. Con notazione più esplicita, l'integrale che si deve calcolare risulta quindi:
= 26098380 terne
"Le dimensioni". Per farci un'idea di che cosa accada. Non ci proponiamo di redigere un catalogo esauriente: esendoci, per esempio, 1/90 gruppi di dimensioni. Che cosa accade al gruppo di dimensioni? Queste dimensioni che hanno ognuno di essa misure determinate sono in continua rotazione.
La rotazione di tali dimensioni rispetto a tale asse statico AB, AC, BC, genera altri gruppi di asse, e dopo la fine di rotazione cè un asse privileggiato, definito "Asse in Contrazione". L'asse privileggiato è quindi un mutamento nel gruppo dei segmenti AB, AC, BC un passaggio da un gruppo Statico a un gruppo in contrazione è quindi un mutamento di asse.
La teoria generale di questa pertubazione prende l'avvio da questo punto di vista e affronta interogativi come <<Quali gruppi possono verificarsi?>>
La risposta può essere molto precisa: Il "Punteggio" che lega la graduatoria della dimensione di appartenenza ed infine "l'incremento di Campo" quando è più grande questo coefficiente, tanto più è maggiore il corrispondente sistema di corpi processati (entrano in gioco le new permutazione). E’ importante sottolineare che, a differenza di una trasformazione di rilevazione classica, in una teoria di questo tipo, la condizione di trasformazione perde il suo significato classico. Il significato essenziale dell’invarianza sta nel fatto che essa influenza la forza del sistema di campo in una trasformazione di rivelazione verticale.
Non tedieremo nessuno di voi con gli aspetti tecnici delle risposte a tali domande, ma è sufficiente sottolineare che essi forniscono la spina dorsale matematica della teoria "Timline Sequenza Temporale", e ne vedremo alcune conseguenze con il progredire della nostra argomentazione.
Saluti...
Lo sviluppo matematico non è però semplicemente una questione di istruzione codificate. Esse posseggono in effetti un significato solo in un contesto in cui possano essere applicate, nello stesso modo in cui un programma per computer è inutile senza un computer che lo faccia girare. Questo è il massimo problema nei giochi d'azzardo non ancora risolto e nessuno conosce realmente la risposta... Buona lettura.
Varie scuole di pensiero spesso, rispettabili e rispettate, si fondono sul misticismo dei numeri, non che non si possono progettare buoni edifici con questi metodi; il fatto è che il senso della progettazione logica svolge il ruolo notevolmente più importante, mentre la cornice mistica è così flessibile che vi si può incorporare qualsiasi progetto con sistemi che non hanno alcuna somiglianza, o le assomigliano solo in virtù di una totale flessibilità.
Quando ci si trova a dover affrontare una situazione complicata, spesso la cosa migliore è quella di porsi a cercare di risolvere i problemi, giusto per avere un'idea della direzione nella quale si sta andando. La nostra scelta potrà quindi essere guidata soltanto da considerazioni nelle quali la valutazione personale svolga un ruolo essenziale, vi sono, ciò nondimeno, soluzioni che tutti vorranno scartare a causa della difficoltà e altre invece che tutti preferiranno a causa delle loro semplicità.
E’ chiaro comunque che il buon senso non fa difetto nemmeno ai più esperti quando in problemi concreti riconoscono che le informazioni disponibili sono qualitativamente diverse fra loro. La differenza essenziale da rilevare è nell’attribuzione del perché: è il nostro pensiero che deve trovare dei rapporti di casualità per descriverli, coordinarli e renderne possibile la previsione. E questo che consente di formalizzare il procedimento induttivo traducendo in forma matematica e logica il concetto di causa che sta alla base di ogni nostra previsione, di ogni nostra formulazione di regolarità statistica. Ecco perché la teoria delle probabilità, logica dell’incertezza, deve essere considerata come la premessa dell’intero ragionamento induttivo.
Tutti i rapporti spaziali a noi noti sono misurabili, cioè possono essere ricondotti alla determinazione di grandezza. Perciò i problemi della geometria possono essere risolti anche cercando metodi per calcolare grandezze incognite da quelle note. Questo è quello che si fa nella geometria analitica, nella quale tutte le figure dello spazio vengono trattare solo come grandezza e sono determinate da altre grandezze. La linea retta è definita come la più breve fra due punti, ciò che è una determinazione di grandezza.
Si può dunque anche partire da quest’aspetto del concetto di spazio, secondo cui la posizione di ogni punto può essere determinata da misura concernente una qualche figura spaziale considerata fissa (sistema di coordinate), e poi esaminare quali particolari caratteristiche compete al nostro spazio, in termini di misure effettivamente eseguibili, e come lo differenziano da grandezze estese di pari molteplicità. Questa via ha il particolare vantaggio che tutte le operazioni che compaiono in essa sono pure determinazioni di grandezza mediante il calcolo, per cui viene a mancare del tutto il pericolo che dati abituali della percezione sono scambiati per necessità del pensiero.
Il numero delle misure necessarie per dare la posizione di un punto è uguale al numero delle dimensioni dello spazio considerato. In una linea sono sufficienti la distanza da un punto fisso e quindi una sola grandezza; in una superficie si devono dare le distanze di due punti fissi, mentre nello spazio tre punti. Le ipotesi che ho dovuto porre alla base del calcolo sono le seguenti.
In primo luogo, per rendere possibile una trattazione matematica, si deve supporre che la posizione di ogni punto di A rispetto a certe figure spaziali considerate immutabili e fisse possa venire determinata da misure di un qualche genere di grandezze spaziali, siano esse linee o linee fra superfici. Come è noto, le misure necessarie per la determinazione della posizione di un qualsiasi punto A prendono il nome di coordinate del punto. Il numero delle coordinate in generale necessarie per la completa determinazione della posizione di un punto qualsiasi definisce il numero di dimensioni dello spazio in esame. Si suppone inoltre che il moto del punto A le grandezze usate quali coordinate variano con continuità.
In secondo luogo la definizione di corpo numerico ovvero di sistema rigido di punti deve essere data, come e necessario, in modo da permettere il confronto di grandezze spaziali per congruenza. La definizione del corpo numerico può venire data semplicemente dal seguente criterio: fra le coordinate di due punti qualunque appartenenti a un corpo numerico deve sussistere un’equazione, che esprime una relazione spaziale e temporale fra i due punti invariante per qualunque movimento del corpo relazione che risulta infine essere la loro distanza e che è la stessa per coppie di punti congruenti. Si definiscono congruenti coppie di punti tali che possono essere fatte coincidere una dopo l’altra con una medesima coppia di punti fissi nello spazio.
Gli elementi A, B, C d’anno tre distinte coppie di punti: AB, AC, BC
Per illustrare meglio come funziona, considererò una soluzione particolare, che sarà possibile, è vero, solo se le condizioni iniziali della distanza della massa estrattiva non subisca alcuna alterazione con lo scorrere del tempo (incremento massa estrazionale), la distanza deve sempre avere le condizioni iniziali, non deve subire alcuna variazione.
Le coordinate della linea AB sono la distanza rappresenta dai valori 0.00012959997. L’osservatore, perciò, dirà cosa rappresenta quel valore?
Se si definisce la quantità di moto di un corpo di tre elementi (che viaggia come se fosse un corpo unico); dal prodotto della sua massa * la sua velocità otteniamo la misura di forza agente sul corpo stesso.
Valori integrali
Distanza estrazionale =
= massa * velocità =
= 0.00012959997 massa * velocità 1666667 = 216
Di conseguenza l’intervallo spaziale =
= massa * velocità =
= 0.00000719999 massa * velocità 1666667 = 12
Da cui segue l’intervallo temporale =
= massa * velocità =
= 0.00002159999 massa massa * velocità 1666667 = 36
Questi numeri non sono stati scelti per semplicità, 216,12, 36, ma non sono molto lontani dal vero. Quel che dobbiamo fare, perciò, è cominciare a formulare domande molto generali, prescindendo il più possibile da ogni connessione con la fisica reale del moto dei corpi numerici. Questo modo di procedere è contrario alle tendenze tradizionali nella dinamica dei corpi numerici, ma ha un senso matematico e scientifico: capire prima la natura generale del problema, poi usare tale comprensione per progettare un attacco frontale.
Tutto questo presenta il vantaggio di un trasferimento di tecnologia, quanto meno specifici sono i nostri assunti sulla dinamica del moto numerico, tanto più largamente applicabili possono essere i nostri risultati. Ci chiediamo quindi: quali sono le conformità del sistema? Qual è il catalogo dei tipi di comportamento possibili in un sistema che possegga tale conformità?
Che cosa dobbiamo calcolare per determinare quale di tali comportamenti possibili si verifichi realmente, e quale sia la sua stabilità? Solo dopo aver risposto a queste domande generali cominceremo a calcolare i valori che ci interessano. Dobbiamo ammettere che non otterremo tutti i particolari che potremmo conseguire con una simulazione numerica completa: questo è il prezzo che dobbiamo pagare. In compenso, però, otterremmo una vasta comprensione matematica non solo di questo sistema, ma di qualsiasi altro sistema con le stesse conformità.
Quel che stiamo dicendo è che ci sono strategie alternative disponibili a seconda di ciò che si vuole conoscere, e che strategie diverse sono efficaci su tipi diversi di problemi. L’applicazione della matematica alla scienza numerica è un processo continuo in cui noi impariamo quali siano gli strumenti migliori per risolvere qualsiasi problema dato. Le generalità della rottura di conformità forniscono non solo un nuovo strumento, bensì un intero nuovo armamentario di strumenti.
Dobbiamo chiederci da dove vengono queste particolari determinazioni che caratterizzano il concetto generale di grandezza estesa. Quando osserviamo un corpo numerico che agisce a distanza su un altro, prima di decidere se si tratta di un’azione diretta e immediata, generalmente guardiamo se vi è qualche connessione di misura tra i due corpi; e se troviamo un nesso che possa render conto dell’interazione osservata.
E’ dunque evidente che in molti casi l’azione tra corpi numerici distanti può essere spiegata da una sequenza di azioni di ciascun elemento di una serie di corpi numerici occupanti lo spazio interposto sul successivo. Tutte queste idee sono antiche e ben note per i veri cultori di statistica, ma la teoria ha assunto la sua forma definitiva soltanto dopo l’introduzione del teorema Timeline Sequenza Temporale.
Per illustrare meglio come funziona questa contrazione, considererò una soluzione quella del segmento AB, che sarà possibile, è vero, solo se le condizioni iniziali del moto sono del tutto eccezionali, ma che potrà comunque servirci d’esempio anche per il resto dei segmenti AC, BC.
Segmento AB
Valori integrali
Distanza estrazionale =
= massa * velocità =
= 0.00012959997 massa * velocità 1666667 = 216
Di conseguenza l’intervallo spaziale =
= massa * velocità =
= 0.00000719999 massa * velocità 1666667 = 12
Da cui segue l’intervallo temporale =
= massa * velocità =
= 0.00002159999 massa * velocità 1666667 = 36
Segmento AB
Valori in contrazione
Distanza estrazionale =
= massa * velocità =
= 0.00004319999 massa * velocità 1666667 = 72
Di conseguenza l’intervallo spaziale =
= massa * velocità =
= 0.00000239999 massa * velocità 1666667 = 4
Da cui segue l’intervallo temporale =
= massa * velocità =
= 0.00000959999 massa * velocità 1666667 = 16
Da queste considerazioni è possibile concludere che il fenomeno che si verifica con lo scorrere del tempo, ossia il fatto che i corpi numerici, la massa estrazionale, gli intervalli spaziali e temporali si contraggono drasticamente su valori integrali, modifica lo spostamento spaziale e temporale.
Lo stato del sistema dipende da tre parametri, di modo che sia possibile rappresentarlo mediante le linee AB, AC, BC . L'insieme delle linee che rappresentano i diversi stati possibili non sarà allora l'intero spazio, ma bensi un numero di regioni disseminati nello spazio. Se assumiamo il determinismo ai primi tre stati , questi debbono essere considerati equiprobabili. Procedendo così, si vede che tutti gli stati che potremmo prima o poi raggiungere non debbono essere considerati equiprobabili, ma come stati possibili in fase di decelerazione AB, AC, BC.

Per quasi un secolo gli studiosi si sono affaticati su questo problema, apportanto grande testimonianza eloquente della rapidità con cui i concetti matematici permeano la cultura umana. E' chiaro a che punto si trovi la questione: ma modificarle è parso necessario. Ovviamente possono esserci altre altre vie, ma che nessuno fino ad oggi a trovato l'idea; quindi preciso, la natura del problema, che in primis portiamo su questa pagine.
E' scontato che con i 90 corpi numerici si vengono a formare 117.480 terne, ma il punto culminante della nostra ricerca e la dimostrazione che dalle ridisposizioni o permutazioni le terne aumentano di numero.
Per esempio, le tre soluzioni a, b, c possono in generale essere permutate in sei modi:
abc, acb, bac, bca, cab, cba, proseguendo su questa strada qualsiasi terna ha le sue sei permutazioni.
Permutazione dellala terna 1-2-3
ridisposizioni: 1-2-3; 1-3-2; 2-1-3; 2-3-1; 3-1-2; 3-2-1
Le permutazioni sono sconosciuti e lontanissime dai cultori di statistica. C'è però un senso molto reale in cui i gruppi di permutazioni possono essere concepite come gruppi di estenzione. Una permutazione è di per sè una trasformazione, non di uno spazio, bensì della collezione di soluzione aggiuntive. E' una ridisposizione, un modo di prenderle e risistemarle.
Si arriva così ad ottenere, dalla terna originaria, le loro 6 permutazioni. Con notazione più esplicita, l'integrale che si deve calcolare risulta quindi:
= 26098380 terne
"Le dimensioni". Per farci un'idea di che cosa accada. Non ci proponiamo di redigere un catalogo esauriente: esendoci, per esempio, 1/90 gruppi di dimensioni. Che cosa accade al gruppo di dimensioni? Queste dimensioni che hanno ognuno di essa misure determinate sono in continua rotazione.
La rotazione di tali dimensioni rispetto a tale asse statico AB, AC, BC, genera altri gruppi di asse, e dopo la fine di rotazione cè un asse privileggiato, definito "Asse in Contrazione". L'asse privileggiato è quindi un mutamento nel gruppo dei segmenti AB, AC, BC un passaggio da un gruppo Statico a un gruppo in contrazione è quindi un mutamento di asse.
La teoria generale di questa pertubazione prende l'avvio da questo punto di vista e affronta interogativi come <<Quali gruppi possono verificarsi?>>
La risposta può essere molto precisa: Il "Punteggio" che lega la graduatoria della dimensione di appartenenza ed infine "l'incremento di Campo" quando è più grande questo coefficiente, tanto più è maggiore il corrispondente sistema di corpi processati (entrano in gioco le new permutazione). E’ importante sottolineare che, a differenza di una trasformazione di rilevazione classica, in una teoria di questo tipo, la condizione di trasformazione perde il suo significato classico. Il significato essenziale dell’invarianza sta nel fatto che essa influenza la forza del sistema di campo in una trasformazione di rivelazione verticale.
Non tedieremo nessuno di voi con gli aspetti tecnici delle risposte a tali domande, ma è sufficiente sottolineare che essi forniscono la spina dorsale matematica della teoria "Timline Sequenza Temporale", e ne vedremo alcune conseguenze con il progredire della nostra argomentazione.
Saluti...
Ultima modifica: