Rookie
Advanced Member >PLATINUM PLUS<
Cio' di cui discetteremo, costituisce le fondamenta sulle quali e' stato edificato il nostro LOTTO Quantitativo, ovvero il LOTTO classico, osservato (e valutato) pero' attraverso un nuovo paradigma nel dominio quantitativo. Il quale, non e' assolutamente il paradigma in auge sin dai primordi, tra i lottofili, che qui assume ovviamente una valenza NULLA. Dato che questo modo di osservare invalso tra i lottofili, ovvero valutare solo (e soltanto) determinate combinazioni caratterizzate da una latenza piu' o meno lunghissima nelle prove {effettuate e/o osservate}, determina che le combinazioni selezionate esporranno (necessariamente) un numero di successi = 0 (zero). Ossia nessuna delle combinazioni selezionate registra un successo nell'arco delle estrazioni analizzate, giusto per intendersi al meglio.
Queste fondamenta sono basate in larga parte su una serie di pilastri, di cui tre sono: (a) le Catene di Markov, (b) l'Indipendenza delle prove, (c) Statistica Bayesiana.
Catene di Markov (CDM)
A. A. Markov (1856 - 1922) nell'anno 1874 inizio a studiare Matematica sotto la guida di un importante Matematico russo in auge in quegli anni, ossia il Grande P. L. Chebishev (1821 - 1894). La carriera di Markov fu rapidissima, infatti ancora studente (anno 1877) con gli studi afferenti alle frazioni continue per risolvere le equazioni differenziali furono premiate con una medaglia d'Oro. Discute la sua tesi nel 1880 e nel giro di pohi anni (1884), consegue il dottorato. Gia' a trenta anni insegna presso l'universita' di San Pietroburgo e poco dopo viene eletto socio della prestigiosa Accademia delle Scienze. Tra i suoi membri, l'Accademia ha annoverato Eulero e Daniel Bernoulli, che gia nel 1738 inizio' a trattare la Probabilita' in Russia redigendo un articolo che verteva sui rischi. Da allora in poi la Probabilita' divenne una delle aree preferite dai matematici russi. Tra i quali spiccano Chebishev e il piu' famoso Andrey Kolmogorov, i quali diedero piena dignita' Matematica alla Probabilita'.
Markov, pubblicò il primo articolo sull'argomento nel 1906 e in seguito lo applico' allo studio della distribuzione delle vocali nell'opera di Alexander Pushkin, Eugene Onegin. All'epoca, il suo lavoro suscitò un discreto interesse. Markov stesso era consapevole dei limiti di applicabilità dei suoi risultati, forse limitati all'analisi dei testi e all'identificazione dello stile degli autori. Aspetto questo, tra innumerevoli altri in molteplici contesti applicativi nel frattempo sviluppati, in uso ancora ai giorni nostri! Quindi qui non stiamo certo parlando di ragionieri praticoni o geometri di qualche sperduto comune...
Teoria delle catene di Markov (CDM)
La teoria delle catene di Markov è uno dei pilastri della Probabilità e della Statistica, utilizzata per modellare sistemi che evolvono nel tempo. Un sistema caratterizzato dalla proprietà di Markov, la quale stabilisce che il futuro stato del sistema stesso, dipende solo dallo stato presente e non dalla sequenza di eventi passati. Questo concetto e' fondamentale in molti campi, tra cui fisica, economia, biologia e ingegneria.
Un caso particolare di questo tipo di sistemi è rappresentato dalle CDM omogenee, nelle quali le Probabilità di Transizione restano costanti nel tempo. Rendendo possibile utilizzare le di matrici di transizione (MDT) per descrivere le relazioni tra gli stati. La MDT reca seco le probabilità di passaggio da uno stato all'altro e, dall'analisi delle potenze di questa matrice, diventa possibile determinare il comportamento a lungo termine del sistema, come la distribuzione stazionaria. Piu' semplicemente, le catene di Markov forniscono strumenti potenti per l'analisi di fenomeni stocastici, rendendo possibile prevedere evoluzioni e stabilire strategie ottimali in numerosi contesti.

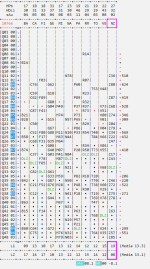
p.s. Da questo quadro, per l'estrazione di questa sera, 4 dicembre, vi sono due sets L1 in evidenza, Z46 e Z72
pp. ss. Era prevedibile il successo della Z52 ?
continua...

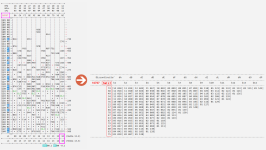
Sinottica afferente alla venus NAZIONALE dopo l'estrazione 10764

Queste fondamenta sono basate in larga parte su una serie di pilastri, di cui tre sono: (a) le Catene di Markov, (b) l'Indipendenza delle prove, (c) Statistica Bayesiana.
Catene di Markov (CDM)
A. A. Markov (1856 - 1922) nell'anno 1874 inizio a studiare Matematica sotto la guida di un importante Matematico russo in auge in quegli anni, ossia il Grande P. L. Chebishev (1821 - 1894). La carriera di Markov fu rapidissima, infatti ancora studente (anno 1877) con gli studi afferenti alle frazioni continue per risolvere le equazioni differenziali furono premiate con una medaglia d'Oro. Discute la sua tesi nel 1880 e nel giro di pohi anni (1884), consegue il dottorato. Gia' a trenta anni insegna presso l'universita' di San Pietroburgo e poco dopo viene eletto socio della prestigiosa Accademia delle Scienze. Tra i suoi membri, l'Accademia ha annoverato Eulero e Daniel Bernoulli, che gia nel 1738 inizio' a trattare la Probabilita' in Russia redigendo un articolo che verteva sui rischi. Da allora in poi la Probabilita' divenne una delle aree preferite dai matematici russi. Tra i quali spiccano Chebishev e il piu' famoso Andrey Kolmogorov, i quali diedero piena dignita' Matematica alla Probabilita'.
Markov, pubblicò il primo articolo sull'argomento nel 1906 e in seguito lo applico' allo studio della distribuzione delle vocali nell'opera di Alexander Pushkin, Eugene Onegin. All'epoca, il suo lavoro suscitò un discreto interesse. Markov stesso era consapevole dei limiti di applicabilità dei suoi risultati, forse limitati all'analisi dei testi e all'identificazione dello stile degli autori. Aspetto questo, tra innumerevoli altri in molteplici contesti applicativi nel frattempo sviluppati, in uso ancora ai giorni nostri! Quindi qui non stiamo certo parlando di ragionieri praticoni o geometri di qualche sperduto comune...
Teoria delle catene di Markov (CDM)
La teoria delle catene di Markov è uno dei pilastri della Probabilità e della Statistica, utilizzata per modellare sistemi che evolvono nel tempo. Un sistema caratterizzato dalla proprietà di Markov, la quale stabilisce che il futuro stato del sistema stesso, dipende solo dallo stato presente e non dalla sequenza di eventi passati. Questo concetto e' fondamentale in molti campi, tra cui fisica, economia, biologia e ingegneria.
Un caso particolare di questo tipo di sistemi è rappresentato dalle CDM omogenee, nelle quali le Probabilità di Transizione restano costanti nel tempo. Rendendo possibile utilizzare le di matrici di transizione (MDT) per descrivere le relazioni tra gli stati. La MDT reca seco le probabilità di passaggio da uno stato all'altro e, dall'analisi delle potenze di questa matrice, diventa possibile determinare il comportamento a lungo termine del sistema, come la distribuzione stazionaria. Piu' semplicemente, le catene di Markov forniscono strumenti potenti per l'analisi di fenomeni stocastici, rendendo possibile prevedere evoluzioni e stabilire strategie ottimali in numerosi contesti.

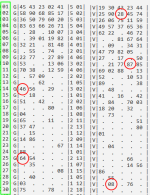
p.s. Da questo quadro, per l'estrazione di questa sera, 4 dicembre, vi sono due sets L1 in evidenza, Z46 e Z72
pp. ss. Era prevedibile il successo della Z52 ?
continua...

Sinottica afferente alla venus NAZIONALE dopo l'estrazione 10764

Ultima modifica: