Frequenze Reali/Teoriche Aspettabilità.

Beppignello · 17 Settembre 2016

teo = Round(55*(17/18)^f,3)

LuigiB · 18 Settembre 2016

ciao Bep , la formula da te postata sembrerebbe quella proposta nel messaggio 8 di Joe ed adattata a 11 ruote.
Forse invece la formula usata dal mio script e presa dal libro del Gorgia va modificata non come avevo detto nella costante di decadimento bensi moltiplicando 90 per il numero delle ruote in esame.
Cosi facendo non so se sia gisto ma almeno i risultati mi suonano bene ..
ho fatto un semplice script che pone al confronto le due formule.

Codice:

Option Explicit
Sub Main
    Dim k , nRetTeoF1 , nRetTeoF2 , nQReali , nQRuote , AF1 , AF2
    
    Dim aTitoli
    
    nQReali = Int(InputBox("inserire laquantita reale dei numeri" ,"QReale" ,1))
    nQRuote = Int(InputBox("Insereire la quantita di ruote" , "QRuote" ,1))
    
    aTitoli = Array ("","Ritardo" ,"PresTeoF1" ,"AttF1", "PresTeoF2", "AttF2")
    Call InitTabella (aTitoli)
    ReDim aV(5)
    
    For k = 0 To 220
        AF1 =  CalcolaAspettabilita( k,nQReali,nRetTeoF1  ,nQRuote )
        AF2 =  CalcolaAspettabilita2( k,nQReali,nRetTeoF2  ,nQRuote )
        aV (1) = k
        aV(2) = nRetTeoF1
        aV(3) = AF1
        aV(4) = nRetTeoF2
        aV(5) = AF2
        
        Call AddRigaTabella(aV)
        
        
    Next
    
    Call Scrivi ("FORMULE CALCOLO QUANTITA TEORICA" , True)
    Call Scrivi ("F1 : T = Round((90*Ruote) * Exp(-(Rit)/17.4952),4)")
    Call Scrivi ("F2 : T = Round((5* Ruote )*(17/18) ^Rit,4)")
    Call Scrivi
    Call Scrivi ("FORMULA CALCOLO ATTENDIBILITA" , True)
    Call Scrivi (" Attendibilita = Reali /(Reali + Teoriche)")
    Call Scrivi
    
    
    Call CreaTabella
    
End Sub
Function CalcolaAspettabilita(Rit,QNumeriAlRit,nRetTeorico , Ruote)
    Dim ValTeorico
    ValTeorico = Round((90*Ruote) * Exp(-(Rit)/17.4952),4)
    nRetTeorico = ValTeorico
    CalcolaAspettabilita = Round(QNumeriAlRit /(ValTeorico + QNumeriAlRit),4)
    
End Function
Function CalcolaAspettabilita2(Rit,QNumeriAlRit,nRetTeorico, Ruote)
    Dim ValTeorico
    ValTeorico = Round((5* Ruote )*(17/18) ^Rit,4)
    nRetTeorico = ValTeorico
    CalcolaAspettabilita2 = Round(QNumeriAlRit /(ValTeorico + QNumeriAlRit),4)
    
End Function

LuigiB · 18 Settembre 2016

a me la seconda formula sembra piu "di manica larga"

LuigiB · 18 Settembre 2016

sempre che la formula per piu ruote sia corretta il seguente script calcola anche l'attendibilità riferita
alla quantita complessiva dei numeri presenti al dato ritardo su tutte le ruote interessate

Codice:

Option Explicit
Sub Main
    Dim r,n,Rit,Asp,nQNumAlRit,nQTeoAlRit ,nQRuote ,AspRuoteInt ,nQNumAlRitRuoteInt ,nQTeoAlRitRuoteInt
    Dim nEstrAnalisi
    nEstrAnalisi = EstrazioneFin
    ReDim aTitoli(9)
    aTitoli(1) = "Ruota"
    aTitoli(2) = "Numero"
    aTitoli(3) = "Ritardo"
    aTitoli(4) = "Aspettabilità"
    aTitoli(5) = "QR"
    aTitoli(6) = "QT"
    aTitoli(7) = "AspRuoteInEsame"
    aTitoli(8) = "QR RuoteEsam"
    aTitoli(9) = "QT RuoteEsam"
    

    
    Call InitTabella(aTitoli)
    
    ReDim aBRuote(0)
    ReDim aRuote(0)
    
    Call ScegliRuote(aRuote,aBRuote )
    
    ReDim aRitRuote( 12 ,90)
    For r = 1 To 12
        If r <> 11 And aBRuote(r) Then
            nQRuote = nQRuote +1
            Call Messaggio(NomeRuota(r))
            ReDim aRitardi(90)
            For n = 1 To 90
                Rit = RitardoEstratto(n,nEstrAnalisi,r)
                aRitRuote( r , n ) = Rit
            Next
        End If
    Next
    
    
    For r = 1 To 12
        If r <> 11 And aBRuote(r) Then
            Call Messaggio(NomeRuota(r))
            
            For n = 1 To 90
                Rit = aRitRuote(r ,n)

                nQNumAlRit = QuantitaNumeriAlRit(Rit,aRitRuote ,r)
                Asp = CalcolaAspettabilita(Rit,nQNumAlRit,nQTeoAlRit ,1)

                nQNumAlRitRuoteInt = QuantitaNumeriAlRitRuoteInt(Rit,aBRuote ,aRitRuote  )
                AspRuoteInt = CalcolaAspettabilita(Rit,nQNumAlRit,nQTeoAlRitRuoteInt,nQRuote)
                
                ReDim aColonne(9)
                aColonne(1) = NomeRuota(r)
                aColonne(2) = n
                aColonne(3) = Rit
                aColonne(4) = Asp
                aColonne(5) = nQNumAlRit
                aColonne(6) = nQTeoAlRit
                aColonne(7) = AspRuoteInt
                aColonne(8) = nQNumAlRitRuoteInt
                aColonne(9) = nQTeoAlRitRuoteInt


                
                Call AddRigaTabella(aColonne)
                Call AvanzamentoElab(1,90,n)
            Next
        End If
    Next
    Call AvanzamentoElab(1,90,1)
    Call Messaggio("Ordinamento in corso")
    
    Scrivi "Ruote in esame : " & StringaRuote(aRuote)
    
    Call CreaTabella(4)
End Sub
Function QuantitaNumeriAlRit(Rit,aRitardi, Ruota)
    Dim k,q
    For k = 1 To 90
        If aRitardi(Ruota ,k) = Rit Then
            q = q + 1
        End If
    Next
    QuantitaNumeriAlRit = q
End Function
Function QuantitaNumeriAlRitRuoteInt(Rit,aBRuote , aRitardi)
    Dim k,q,r
    
    For r = 1 To 12
        If aBRuote (r) Then
            For k = 1 To 90
                If aRitardi(r ,k) = Rit Then
                    q = q + 1
                End If
            Next
        End If
    Next
    QuantitaNumeriAlRitRuoteInt = q

End Function
Function CalcolaAspettabilita(Rit,QNumeriAlRit,nRetTeorico ,Ruote)
    Dim ValTeorico
    ValTeorico = Round((90*Ruote) * Exp(-(Rit)/17.4952),4)
    nRetTeorico = ValTeorico
    CalcolaAspettabilita = Round(QNumeriAlRit /(ValTeorico + QNumeriAlRit),4)
    
End Function
Function CalcolaAspettabilita2(Rit,QNumeriAlRit,nRetTeorico,Ruote)
    Dim ValTeorico
    ValTeorico = Round((5*Ruote)*(17/18) ^Rit,9)
    nRetTeorico = ValTeorico
    CalcolaAspettabilita2 = Round(QNumeriAlRit /(ValTeorico + QNumeriAlRit),4)
    
End Function

Beppignello · 18 Settembre 2016

ciao LuigiB

provo a farci sopra qualche ragionamento, grazie

F2 : T = Round((5* Ruote )*(17/18) ^Rit,4)

Joe91 · 18 Settembre 2016

Buon giorno a tutte/i.

Si, la forma è quella ma nella sostanza emergono piccole differenze.

La curva che bisogna ottenere in prima approssimazione è "una poissoniana".

Se si vuole essere precisi ... quella di una binomiale.

Per un semplicissimo riscontro sarà utile uno sguardo al grafico presente su

Wikipedia Distribuzione di Poisson.

Nel confronto tra i grafici che ho proposto (al messaggio #30)

Ovvero quelli ricavati dalle tabelle fornite da Luigi ...

e l' immagine presente su wikipedia è chiaro che "la curva"

(la poissoniana in funzione del Lambda) è quella per il 5 come 5 sono gli estratti.

Perchè essa è molto simile a quella in funzione del 4 presente in enciclopedia in questo grafico.

Perchè si usa quasi sempre la poissoniana piuttosto che la binomiale ?

Semplice. Perchè il calcolo ovvero la formula da calcolarsi (specie quando il calcolo era manuale)

è molto-molto-molto più semplice quello della poissoniana rispetto a quello della binomiale.

Il mio modesto parere è che si calcola il N.E.T. o le P.T.

poi il risultato lo si moltiplica per il numero di ruote.

Quindi se come detto a ritardo 55 abbiamo 0.23 Estratti Teroici ...

contando quelli di un intero tabellone

ci si attende di trovarne 10 11 volte tanti

cioè 2,3 / 2.53.

LuigiB · 18 Settembre 2016

allora osservando il suggeriemnto di Joe che dice di moltiplicare il valore teorico calcolato per la singola ruota per la quantita di ruote esaminate ripropongo lo script del confronto tra le due formule
con tabella comparativa e grafico...
E' giusto cosi Joe ?

Codice:

Option Explicit
Sub Main
    Dim k,nRetTeoF1,nRetTeoF2,nQReali,nQRuote,AF1,AF2
    
    Dim aTitoli
    
    nQReali = Int(InputBox("inserire laquantita reale dei numeri","QReale",1))
    nQRuote = Int(InputBox("Insereire la quantita di ruote","QRuote",1))
    
    aTitoli = Array("","Ritardo","PresTeoF1","AttF1","PresTeoF2","AttF2")
    Call InitTabella(aTitoli)
    ReDim aV(5)
    
    ReDim aPTeoF1(220)
    ReDim aPTeoF2(220)
    
    For k = 0 To 220
        AF1 = CalcolaAspettabilita(k,nQReali,nRetTeoF1,nQRuote)
        AF2 = CalcolaAspettabilita2(k,nQReali,nRetTeoF2,nQRuote)
        
        aPTeoF1 (k) =nRetTeoF1
        aPTeoF2 (k) =nRetTeoF2
        
        aV(1) = k
        aV(2) = nRetTeoF1
        aV(3) = AF1
        aV(4) = nRetTeoF2
        aV(5) = AF2
        
        Call AddRigaTabella(aV)
        
        
    Next
    
    Call Scrivi("FORMULE CALCOLO QUANTITA TEORICA",True)
    Call Scrivi("F1 : T = Round((90*Ruote) * Exp(-(Rit)/17.4952),4)")
    Call Scrivi("F2 : T = Round((5* Ruote )*(17/18) ^Rit,4)")
    Call Scrivi
    Call Scrivi("FORMULA CALCOLO ATTENDIBILITA",True)
    Call Scrivi(" Attendibilita = Reali /(Reali + Teoriche)")
    Call Scrivi
    
    
    Call CreaTabella
    
    
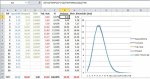
    Call PreparaGrafico("Confronto presenze teoriche" ,0 , 220 ,0, 100 * nQRuote,10 ,  (100* nQRuote)/10 )
    
    ' prima riga
    ReDim aV(220,2)
    
    For k = 0 To 220
        aV(k,1) = k
        aV(k,2) =  aPTeoF1 (k)
        
        
    Next
    Call DisegnaLineaGrafico(aV, 1,"F1")

    ReDim aV(220,2)
    
    For k = 0 To 220
        aV(k,1) = k
        aV(k,2) =  aPTeoF2 (k)
        
        
    Next
    Call DisegnaLineaGrafico(aV, 2,"F2")




    ' scrive grafico nell'output
    
    Call InserisciGrafico
    
    Scrivi "Asse X : Ritardo"
    Scrivi "Asse Y : Presenze"
    

    
End Sub
Function CalcolaAspettabilita(Rit,QNumeriAlRit,nRetTeorico,Ruote)
    Dim ValTeorico
    ValTeorico = (Round(90 * Exp(-(Rit)/17.4952),4))*Ruote
    nRetTeorico = ValTeorico
    CalcolaAspettabilita = Round(QNumeriAlRit /(ValTeorico + QNumeriAlRit),4)
    
End Function
Function CalcolaAspettabilita2(Rit,QNumeriAlRit,nRetTeorico,Ruote)
    Dim ValTeorico
    ValTeorico = (Round(5*(17/18) ^Rit,4)) * Ruote
    nRetTeorico = ValTeorico
    CalcolaAspettabilita2 = Round(QNumeriAlRit /(ValTeorico + QNumeriAlRit),4)
    
End Function

Joe91 · 18 Settembre 2016

Ciao Luigi.

Scusa se non ho riposto ma ho problemi con il modem.

Intanto espongo diversamente.

al primo ritardo se sono Attesi 5 Teorici in una ruota ...

in 10/11 ... 50/55

Così se come detto a ritardo 55 la teroria prevede

0.23 estratti moltilicandolo per 10

dovrebbero essere 2.3

e tutto questo dovrebbe trovare riscontro

nel tabellone analitico

LuigiB · 19 Settembre 2016

Ciao Joe allora mi sa che non ho capito bene la formula da usare..vedi se riesci a scriverla tu la finzioncina per il calcolo teorico cosi vedo...

Beppignello · 19 Settembre 2016

io ottengo quanto segue:

la formula è sempre la stessa

ValTeorico = Round(55 * Exp(-(Ritardo/17.4952),4)

al ritardo 54 ottengo 2,5112 presenze teoriche

Joe91 · 20 Settembre 2016

LuigiB;n2005058 ha scritto:
Ciao Joe allora mi sa che non ho capito bene la formula da usare..vedi se riesci a scriverla tu la finzioncina per il calcolo teorico cosi vedo...

Ciao Luigi.

Secondo me, dallo studio della distibuzione poissonina si ricava "il modo".

Sempre secondo il mio modeto parere ...

Del numero degli Estratti Teoricamente Previsti al ritardo "R"

essendo essi equiprobabili cadono ognuno con la stessa probabilità di 1/18.

Quindi le "Presenze Teoriche" sono 1/18 delle "Presenze Teoriche"

se non le si distingue semanticamente.

Dovremmo usare una classificazione e misurazione "condivise".

Come ad esempio è per Spazio,Tempo, Velocità, Accelerazione.

"Misurando" ogni realtà attribuendole un "Valore" ed un "Nome".

Valore, misurato con l' appropriato strumento ed "Unità di Misura".

così come lo spazio ha il "metro", il tempo ha il "secondo".

Anche, la velocità e l'accelerazione hanno opportune unità di misura ovvero

"Unità di misura" derivate da quelle fondamentali.

Dunque il loro "nome" ... diverso e caratteristico ...

acquista un "valore" che si sa cos'è.

Per cui:

La velocità è lo spazio percorso nell' unità di tempo.

Tipicamente la si misura in "metri al secondo".

L' accelerazione è la variazione della velocità nell'unità di tempo.

E' misurata in "metri al secondo-quadrato".

Dicevo che "Frequenza" non vuol dire nulla senza unità di misura.

Se non stabiliamo, per esempio la differenza

che c'è tra il Kilovatt ed il Kilovatt/ora

essi sembreranno la stessa cosa.

Mentre invece uno è una "potenza" l'altro è un "lavoro".

Cioè si confonde il lavoro con la potenza dimenticando il tempo.

Senza classificare ... ci incartiamo.

Con questa premessa se si espande il "Teorico"

a più Ruote e/o a più Estrazioni.

Semplicemente si moltiplica questo "Numero di Estratti Teorico"

(al ritardo "R") per il numero di ruote e/o di estrazioni.

Ma questo è un terzo passaggio ...

bisogna prima considerare anche il ritardo naturale (caratteristico)

senza perderci per strada questo secondo parametro.

Tenendo anche presente che se si considerano ritardi differenti ...

cioè delle "fascie di ritardo" si devono anche considerare

le variazioni presenti tra questi livelli di ritardo.

Altrimenti il tutto diventa argomento babilonioso.

Giustamente ... hai rilevato confusione anche nei termini

("exp" in particolare) indicato come elevazione a potenza ...

nelle veci di "^" mentre fors'era "e" o numero di Nepero o di Eulero.

(Poi però non utilzzato nei calcoli).

Ho inserito dunque una sintesi grafica comprensiva

della fourmula che hai richiesto.

"FdF" è provvisoriamente "Frequenza della Frequenza".

Anche se sembra un ritardo ... è un altra cosa.
_

i legend · 20 Settembre 2016

Ciao scusate se mi intrometto
La funzione di spaziometria
Quantitateonumericombalritx è corretta o è quella che state cercando di perfezionare?

Joe91 · 20 Settembre 2016

Ciao i legend. Nel grafico sopra c'è un confronto tra le tabelle di spaziometria quelle presenti nei testi universitari di statistica ... la poissoniana ed il calcolo con la binomiale. Coincidono. Ma c'è anche un discorso più ampio e "trasversale" che non può essere contenuto tutto in un si.

Joe91 · 20 Settembre 2016

Come dicevo a Luigi ...

Dal calcolo della poissoniana si evidenzia bene che

" * 90 " è praticamente esterno alla formula e ...

serve a ottenere la distribuzione "per 90".

Ma questo "90" non sono gli estratti.

Infatti nella colonna accanto si ha la stessa distribuzione

in 100 centesimi ... cioè 1.

Come dire a che se in ogni condominio la somma dei millesimi è 1000.

Di questo 1000 ...

100 millesimi in un condominio, non sono i 100 millesimi di un altro condominio.

Anche se entrambi i proprietari di questi 100 millesimi

posseggono ambedue il 10 % del valore del loro condominio,

le loro proprietà possono avere valori molto differenti

se misurate in Euro.

Quindi non parliamo più di ritardi o di frequenze ma di "distribuzioni".

Secondo regole matematiche e statistiche.

i legend · 20 Settembre 2016

Ciao Joe grazie per le risposta .
Vi seguo con interesse

Joe91 · 21 Settembre 2016

Al messaggio #18 abbiamo visto che possiamo calcolare

in più modi 0.23 per il ritardo 54.

Unito a quanto chiedeva ilegend è ottimo spunto per verificare.

Una Ruota a caso: sempre Bari.

Un numero a caso, sempre grande, quante sono 1000 estrazioni.

Se tutto è ok sono 230 casi da giocare. 0.23 * 1000.

E' ... lo script di un metodo statistico cioè quello che gioca

per un Colpo il ritardo di rigo.

Codice:

Option Explicit
Sub Main
'Controllo 54. Script By Joe
Dim Ini,Fin,Es,Rit,N,K
Dim KK,Nu(1),Ru(1),Po(1)
Rit = 54 : Ru(1) = 1 : Po(1) = 1
Ini = EstrazioneFin - 999 : Fin = EstrazioneFin
For Es = Ini To Fin
Messaggio DataEstrazione(Es)
AvanzamentoElab Ini,Fin,Es
K = 0
For N = 1 To 90
If EstrattoRitardoTurbo(Ru(1),N,1,Es) = Rit Then
K = K + 1
Nu(1) = N
ImpostaGiocata K,Nu,Ru,Po,1,1
End If
Next
If K > 0 Then
KK = KK + 1
Scrivi String(100,"-") & FormatSpace(KK,6,True),True
Gioca Es,True
End If
Next
ScriviResoconto
End Sub

Attenzione: Non inganni la coincidenza.

L' alea è pur sempre presente.

Anche se, su un mumero molto grande di estrazioni,

cioè quelle di circa 6 Anni,

fa si, che i valori teorici e reali siano quasi coincidenti.

Joe91 · 21 Settembre 2016

Dopo aver controllato ...

La prevedibiltà statistica delle Frequenze dei Ritardi,

riscontrando, la perfetta coincidenza con quanto ipotizzato.

Questo script invece è utile per controllare le Frequenze.

Codice:

Option Explicit
Sub Main
'Campioni di Presenze. Script By Joe
Dim Ini,Fin,N,R,F
Dim FR(90)
R = BA_ : Ini = 9215 - 89 : Fin = 9215
Scrivi NomeRuota(R),True
Scrivi "Num . Freq.",True
For N = 1 To 90
F = EstrattoFrequenza(R,N,Ini,Fin)
Scrivi N & Chr(9) & F
FR(F) = FR(F) + 1
Next
Scrivi
Scrivi "Freq. FdF",True
For F = 0 To 15
Scrivi F & Chr(9) & FR(F)
Next
End Sub

... dirò come l'ho utilizzata.

Joe91 · 22 Settembre 2016

Abbiamo detto che Luigi ha fornito ...

la tabella della Distribuzione Binomiale.

Abbiamo controllato, sia con l' approsssimazione di Poisson,

sia con il calcolo vero e proprio per la binomiale. che fosse giusta.

La si è tradotta in grafico che è una traccia di riferimento.
_

Sovrapponendoci i dati reali prodotti dallo script del messaggio #37

Si osservano alcune cose:

C' è ancora una "Frequenza della Frequenza (Zero)" = "1".

Ovvero è una situazione ancora incompleta.

MA ... la curva reale che si produce è ben aderente il modello teorico.

Quindi sono confrontabili.

Sovrapponibili.

Tralasciando tutto cio che le rende simili ...

Le uniche "anomalie" generate dall' alea,

fanno si che siano sottotraccia i numeri presenti 3 e 4 volte.

Quindi ... con il trascorre delle estrazioni taluni di essi ...

dovrebbero incrementare le loro presenze.

genios · 22 Settembre 2016

Non vorrei sbagliare ma mi sembra che il Gorgia distinguesse tra' aspettabilità e attendibilità . Vi faccio sapere intanto siccome ho degli esempi proprio del Gorgia potreste secondo le formule applicate da voi quale sia l' attendibilità di un estratto che manchi da 167 estrazioni .

Saluti EUGENIO

vincenzo4221 · 22 Settembre 2016

Ciao Eugenio , vi posto un brano di un articolo comparso su lottogazzetta che dà chiarimenti in merito:

"L'aspettabilità cosi come l'attendibilità è un valore che va da 0 a 1 , ma mentre la prima scaturisce da un rapporto fra una statistica teorica e una pratica ed entrambe basate sullo stesso concetto analitico , la seconda è il frutto fra due statistiche fra loro diverse."

Acc. quanto ho studiato! peccato non aver mai trovato una persona che con le sue conoscenze informatiche avrebbe già da molto tempo potuto affrontare delle tematiche che vedo sviluppare solo adesso dopo anni e questo purtroppo devo dire per egoismo ben celato.
Comunque "meglio soli che male accompagnati" mi son detto , meno male che vedo col tempo avvicinarsi al forum delle persone che oltre a prendere cercano anche di dare..

Frequenze Reali/Teoriche Aspettabilità.

Beppignello

Guest

LuigiB

Guest

LuigiB

Guest

LuigiB

Guest

Beppignello

Guest

Advanced Member >PLATINUM PLUS<

LuigiB

Guest

Advanced Member >PLATINUM PLUS<

LuigiB

Guest

Beppignello

Guest

Allegati

Advanced Member >PLATINUM PLUS<

Premium Member

Advanced Member >PLATINUM PLUS<

Advanced Member >PLATINUM PLUS<

Premium Member

Advanced Member >PLATINUM PLUS<

Advanced Member >PLATINUM PLUS<

Advanced Member >PLATINUM PLUS<

Advanced Member >PLATINUM<

Advanced Member >PLATINUM<