B
Beppignello
Guest
Appunti da Wikipedia:
https://it.wikipedia.org/wiki/Algoritmo
[h=3]Esempio: studio della complessità di risoluzione dei sistemi lineari[modifica | modifica wikitesto][/h] [TABLE="class: noprint"]
[TR]
[TD]
[/TD]
[TD]Lo stesso argomento in dettaglio: Sistema di equazioni lineari.[/TD]
[/TR]
[/TABLE]
Vogliamo trovare un algoritmo efficiente per risolvere un sistema lineare di
equazioni in
incognite (anche 100, 1000...). Dobbiamo cioè valutare, tra tutti gli algoritmi risolutivi disponibili, quello che impiega meno tempo e consuma meno spazio degli altri. L'Algebra ci offre due importanti metodi risolutivi di enorme interesse ai fini dello studio della complessità degli algoritmi.
NOTA negli esempi si tiene conto che il sistema sia univocamente determinato. In sede di approfondimento è possibile conoscere quali sono le condizioni affinché gli algoritmi che stiamo per esporre sono applicabili [TABLE="class: noprint"]
[TR]
[TD]
[/TD]
[TD]Lo stesso argomento in dettaglio: Regola di Cramer.[/TD]
[/TR]
[/TABLE]
La Regola di Cramer permette la risoluzione di un sistema lineare nel modo più semplice grazie a una singola definizione:
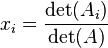dove
è la matrice formata sostituendo la iesima colonna di
con il vettore delle incognite. Il determinante della matrice può essere calcolato a priori, dunque serve solo il calcolo di
determinanti per risolvere il sistema. Il determinante è solitamente definito tramite lo sviluppo di Laplace, che fornisce direttamente un algoritmo ricorsivo:
dove
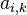è l'elemento di coordinat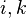e
e
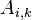è il minore ottenuto sopprimendo la
-esima riga e la
-esima colonna. La complessità di questo algoritmo per il calcolo del determinante è
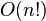, perché per ogni determinante di ordine
si devono calcolare
determinanti di ordine
.
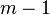Vengono perciò utilizzati altri algoritmi con complessità migliore. (Incidentalmente, tali algoritmi sono anche alla base di metodi più efficienti per il calcolo del determinante). Uno di questi è il metodo di eliminazione di Gauss, basato su due importanti principi.
Il primo è che due sistemi lineari
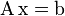e
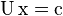sono uguali se
si ottiene sostituendo le righe e le colonne di
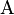con loro combinazioni lineari e gli elementi di
sono combinazioni lineari degli elementi di
in base ai coefficienti di
.
Il secondo è che per risolvere un sistema triangolare (dove cioè la matrice dei coefficienti gode della proprietà di triangolarità) è sufficiente utilizzare l'algoritmo di sostituzione in avanti o all'indietro (la complessità computazionale è
).
Si dimostra che per trasformare il sistema in triangolare occorre un algoritmo la cui complessità è
. Applicando a questo sistema l'algoritmo di sostituzione diretta si trovano le soluzioni esatte del sistema, e si dimostra che la complessità totale dell'algoritmo di Gauss è sempre
.
Per quanto riguarda la complessità spaziale:
https://it.wikipedia.org/wiki/Algoritmo
[h=3]Esempio: studio della complessità di risoluzione dei sistemi lineari[modifica | modifica wikitesto][/h] [TABLE="class: noprint"]
[TR]
[TD]
[TD]Lo stesso argomento in dettaglio: Sistema di equazioni lineari.[/TD]
[/TR]
[/TABLE]
Vogliamo trovare un algoritmo efficiente per risolvere un sistema lineare di
NOTA negli esempi si tiene conto che il sistema sia univocamente determinato. In sede di approfondimento è possibile conoscere quali sono le condizioni affinché gli algoritmi che stiamo per esporre sono applicabili [TABLE="class: noprint"]
[TR]
[TD]
[TD]Lo stesso argomento in dettaglio: Regola di Cramer.[/TD]
[/TR]
[/TABLE]
La Regola di Cramer permette la risoluzione di un sistema lineare nel modo più semplice grazie a una singola definizione:
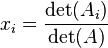
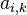
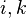
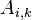
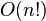
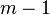
Vengono perciò utilizzati altri algoritmi con complessità migliore. (Incidentalmente, tali algoritmi sono anche alla base di metodi più efficienti per il calcolo del determinante). Uno di questi è il metodo di eliminazione di Gauss, basato su due importanti principi.
Il primo è che due sistemi lineari
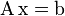
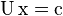
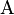
Il secondo è che per risolvere un sistema triangolare (dove cioè la matrice dei coefficienti gode della proprietà di triangolarità) è sufficiente utilizzare l'algoritmo di sostituzione in avanti o all'indietro (la complessità computazionale è
Si dimostra che per trasformare il sistema in triangolare occorre un algoritmo la cui complessità è
Per quanto riguarda la complessità spaziale:
- l'algoritmo basato sulla regola di Cramer richiede soltanto una variabile aggiuntiva, dove memorizzare il determinante della matrice dei coefficienti, dunque la sua complessità è minima: (cioè
per memorizzare la matrice dei coefficienti,
per memorizzare il vettore dei termini noti e le soluzioni, più uno spazio anch'esso pari a
per il calcolo dei determinanti)
- l'algoritmo di Gauss non richiede altro spazio oltre a quello necessario per memorizzare la matrice dei coefficienti e il vettore dei termini noti. Al termine dell'algoritmo il vettore dei termini noti conterrà la soluzione. Pertanto la sua complessità spaziale è anch'essa minima: .
Ha centrato anche due previsioni al secondo colpo nell'altro mio thread "lunghette..." 
Grande beppe e ciao sky! 
