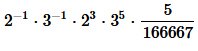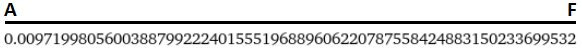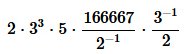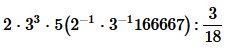Asuniverso
Advanced Member >PLATINUM PLUS<
Viaggio all’interno della struttura del modello “TIMELINE SEQUENZA TEMPORALE”
Il quarto periodo
Ci si può chiedere se la statistica non sia alla volta di una nuova perturbazione? Ciò non significa che le conquiste di ieri sono compromesse o debbano essere abbandonate, ma a tutte queste audacie se ne vogliano aggiungere ancora delle altre. E’ ciò costituirebbe un nuovo incremento alla statistica. Innanzitutto dobbiamo spiegare come si è potuti giungere a una visione di questa portata. Consideriamo la teoria TST (timeline sequenza temporale): è scontato che, se dovessimo analizzare i 90 corpi numerici, quest’ultimi hanno dei limiti strutturali, quindi per non avere dei limiti adottiamo le 117.480 terzine (corpo di tre elementi, ma che viaggiano come un corpo unico) che offrono un cammino maggiore per le misurazione. Il carattere di queste misurazione sortisce l’effetto di stabilire una certa distribuzione media delle estrazione, sia per quanto riguarda la loro direzione spaziale, sia per quanto riguarda la loro intensità temporale; qualora venga perturbata, questa distribuzione media tende a ristabilirsi con l’inestricabile complessità del moto delle terzine, dalla loro misurazione si è in grado di distinguere soltanto i valori sotto l’equilibrio di misura statistico, le quali sono effetto del gioco delle probabilità e delle leggi dei grandi numeri.
Immaginiamo ora di andare da A sino al punto E
A-------------------------------------------------------------------E
Per stabilire la posizione di un corpo numerico (corpo di tre elementi che viaggia come un corpo unico), facciamo uso dell’equazione sottostante, che chiameremo equazione di riferimento, e misuriamo il cumulo estrattivo dal punto A al punto E.
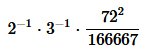
La relazione stabilisce la posizione dal punto A al punto E, dicendo che esso si trova ad una distanza d'estrazione, quantizzata in misura decimale:
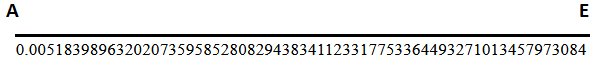
Ora, poiché conosciamo la distanza d'estrazione, analogamente l’intervallo spaziale tra A e E è definita dalla seguente equazione:
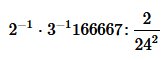
da cui segue la linea di intervallo spaziale

Conoscendo l’intervallo spaziale tra A e E, possiamo calcolare l’intervallo temporale tra A e E dalla seguente equazione:
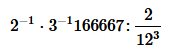
si otterrà la linea di intervallo temporale

Quanto è stato esposto, tra il primo, secondo, terzo e quarto si riferisce però a solo quattro periodi: quello in cui il moto numerico avviene nella direzione di A-B, A-C, A-D ed estendersi sino ad A-E. Le quattro condizioni, della costanza di tali espressioni, non bastano quindi più a fare restare costante l’espressione trovata da A-B, A-C, A-D, A-E. In altre parole per avere una misurazione completa del sistema, dobbiamo includere A-B, A-C, A-D, A-E, A-F. Di conseguenza la misura A-F è la somma delle sue energie di moto lungo tutto l’asse; questo ci conduce a identificare il principio di conservazione del moto equivalente a quello di conservazione delle distanze in tutti i 5 periodi.
Segue.
Saluti…
Il quarto periodo
Ci si può chiedere se la statistica non sia alla volta di una nuova perturbazione? Ciò non significa che le conquiste di ieri sono compromesse o debbano essere abbandonate, ma a tutte queste audacie se ne vogliano aggiungere ancora delle altre. E’ ciò costituirebbe un nuovo incremento alla statistica. Innanzitutto dobbiamo spiegare come si è potuti giungere a una visione di questa portata. Consideriamo la teoria TST (timeline sequenza temporale): è scontato che, se dovessimo analizzare i 90 corpi numerici, quest’ultimi hanno dei limiti strutturali, quindi per non avere dei limiti adottiamo le 117.480 terzine (corpo di tre elementi, ma che viaggiano come un corpo unico) che offrono un cammino maggiore per le misurazione. Il carattere di queste misurazione sortisce l’effetto di stabilire una certa distribuzione media delle estrazione, sia per quanto riguarda la loro direzione spaziale, sia per quanto riguarda la loro intensità temporale; qualora venga perturbata, questa distribuzione media tende a ristabilirsi con l’inestricabile complessità del moto delle terzine, dalla loro misurazione si è in grado di distinguere soltanto i valori sotto l’equilibrio di misura statistico, le quali sono effetto del gioco delle probabilità e delle leggi dei grandi numeri.
Immaginiamo ora di andare da A sino al punto E
A-------------------------------------------------------------------E
Per stabilire la posizione di un corpo numerico (corpo di tre elementi che viaggia come un corpo unico), facciamo uso dell’equazione sottostante, che chiameremo equazione di riferimento, e misuriamo il cumulo estrattivo dal punto A al punto E.
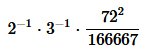
La relazione stabilisce la posizione dal punto A al punto E, dicendo che esso si trova ad una distanza d'estrazione, quantizzata in misura decimale:
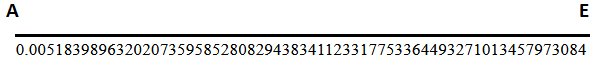
Ora, poiché conosciamo la distanza d'estrazione, analogamente l’intervallo spaziale tra A e E è definita dalla seguente equazione:
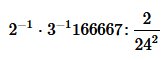
da cui segue la linea di intervallo spaziale
Conoscendo l’intervallo spaziale tra A e E, possiamo calcolare l’intervallo temporale tra A e E dalla seguente equazione:
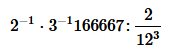
si otterrà la linea di intervallo temporale
Quanto è stato esposto, tra il primo, secondo, terzo e quarto si riferisce però a solo quattro periodi: quello in cui il moto numerico avviene nella direzione di A-B, A-C, A-D ed estendersi sino ad A-E. Le quattro condizioni, della costanza di tali espressioni, non bastano quindi più a fare restare costante l’espressione trovata da A-B, A-C, A-D, A-E. In altre parole per avere una misurazione completa del sistema, dobbiamo includere A-B, A-C, A-D, A-E, A-F. Di conseguenza la misura A-F è la somma delle sue energie di moto lungo tutto l’asse; questo ci conduce a identificare il principio di conservazione del moto equivalente a quello di conservazione delle distanze in tutti i 5 periodi.
Segue.
Saluti…
Ultima modifica: