Buchi e....dintorni

[carlomagnani]

Scusate la venus che parlate qual'e?

Penso sia quella di ba dove rimangono 3 numeri 47 36 62.Chiederei anch'io se posso la situazione di fi e ge che ultimamente erano bollenti sopratutto fi.Grazie infinite studio molto affascinante ma per ora difficile per me

 

[Rookie]

Lo scenario delle 11 venus, offre diversi spunti per le quali riflettere, ma... dal punto di vista Lotto Quantitativo (QuantLotto) , in questo momento storico e' la venus sotto il Vesuvio a essere intrigante davvero. Qui sotto e' lo scenario generale, in cui s'incastona l'anomalia temporanea, la quale dovrebbe regredire normalizzandosi velocemente:

Dunque occhio (in primis) agli LZero deinde agli LUno... ai piedi del Vesuvio. Buon vento e pale a prora.


p.s. In parole semplici, visto che gli LZero partenopei sono in forte sofferenza, dunque e' credibile che almeno 4 degli Luno provvedano alle necessita' del Caso, per regredire verso la norma di cui al calcolo teorico. A cio' si aggiunge che la situazione gia' anomala, sic stante rebus, in due estrazioni, sara' ancor piu' negativa rispetto a quanto esposto e proposto con questo post. E un occhio ai sovrappopolati sets L3 da q18 a q31

 

[andy881]

Lo scenario delle 11 venus, offre diversi spunti per le quali riflettere, ma... dal punto di vista Lotto Quantitativo (QuantLotto) , in questo momento storico e' la venus sotto il Vesuvio a essere intrigante davvero. Qui sotto e' lo scenario generale, in cui s'incastona l'anomalia temporanea, la quale dovrebbe regredire normalizzandosi velocemente:

Dunque occhio (in primis) agli LZero deinde agli LUno...


Vedi l'allegato 2293928

Scusa ma mia ignoranza ma non riesco ad identificare gli lo

 

[Rookie]

Scusa ma mia ignoranza ma non riesco ad identificare gli lo

Non devi identificare gli LZero, devi solo contare quelli che vedi per capire e delimitare l'area rappresentata nel turt sulle quali focalizzarti...

p.s. Mi ripeto (con te), visto che l'ho gia' scritto in precedenza, se non hai la voglia di leggere e capire riesce difficile seguire la logica sottesa dal nostro modo di osservare e studiare l'Italico gioco del Lotto

 

[Rookie]

Lo scenario delle 11 venus, offre diversi spunti per le quali riflettere, ma... dal punto di vista Lotto Quantitativo (QuantLotto) , in questo momento storico e' la venus sotto il Vesuvio a essere intrigante davvero. Qui sotto e' lo scenario generale, in cui s'incastona l'anomalia temporanea, la quale dovrebbe regredire normalizzandosi velocemente:

Dunque occhio (in primis) agli LZero deinde agli LUno... ai piedi del Vesuvio. Buon vento e pale a prora.

p.s. In parole semplici, visto che gli LZero partenopei sono in forte sofferenza, dunque e' credibile che almeno 4 degli Luno provvedano alle necessita' del Caso, per regredire verso la norma di cui al calcolo teorico. A cio' si aggiunge che la situazione gia' anomala, sic stante rebus, in due estrazioni, sara' ancor piu' negativa rispetto a quanto esposto e proposto con questo post. E un occhio ai sovrappopolati sets L3 da q18 a q31

NAPOLI:

Un'immagine e' piu' eloquente di 1000 parole. Il primo tra gli L1 e' arrivato... accompagnandosi a due sfere dai sets L3... nella fascia
indicata epperoche' non e' ancora finita sotto al vesuvio. Ci saranno ulteriori scosse sismiche...di assestamento!

 

[Ciccio90]

NAPOLI:

Un'immagine e' piu' eloquente di 1000 parole. Il primo tra gli L1 e' arrivato... come anche (insieme) a due sfere dai sets L3... nella fascia indicata

Vedi l'allegato 2293945

Superlativo, grande maestro

 

[SatuRno17]

Ciao a tutti,
Volevo complimentarmi con voi per i vostri studi che state portando avanti da anni e soprattutto perché questo è uno dei pochi threads (forse l'unico) in cui ogni cosa è spiegata in maniera chiara e limpida. Buon proseguimento!

 

[Elleuca]

Buongiorno Rookie e buon sabato. Mi complimento anch'io con te per l'ottima ipotesi andata a buon fine al primo colpo. Alla fine erano poche sfere allo stato L1 da abbinare a poche sfere allo stato L3 . Una scrematura sostanziale rispetto alla totalità delle possibilità. È questo che ha reso l'ipotesi(la tua) oltre che vera ,strepitosa!
A presto

 

[Elleuca]

Penso sia quella di ba dove rimangono 3 numeri 47 36 62.Chiederei anch'io se posso la situazione di fi e ge che ultimamente erano bollenti sopratutto fi.Grazie infinite studio molto affascinante ma per ora difficile per me

Ciao a tutti,
Volevo complimentarmi con voi per i vostri studi che state portando avanti da anni e soprattutto perché questo è uno dei pochi threads (forse l'unico) in cui ogni cosa è spiegata in maniera chiara e limpida. Buon proseguimento!

Buongiorno e benvenuti in questo thread a carlomagnani e a SatuRno17. Buona permanenza e buona lettura. Grazie

 

[Elleuca]

Penso sia quella di ba dove rimangono 3 numeri 47 36 62.Chiederei anch'io se posso la situazione di fi e ge che ultimamente erano bollenti sopratutto fi.Grazie infinite studio molto affascinante ma per ora difficile per me

Firenze e Genova si stanno preparando . In generale ci vogliono un po' di estrazioni affinché il quadro si popoli di L1 da cui poi attingere le sfere che creeranno il Pb. Ecco perché sono state momentaneamente parcheggiate. Ma ora mi sembra che i tempi siano maturi.

 

[Rookie]

Buongiorno Rookie e buon sabato. Mi complimento anch'io con te per l'ottima ipotesi andata a buon fine al primo colpo. Alla fine erano poche sfere allo stato L1 da abbinare a poche sfere allo stato L3 . Una scrematura sostanziale rispetto alla totalità delle possibilità. È questo che ha reso l'ipotesi(la tua) oltre che vera ,strepitosa!
A presto

Buongiorno Caro Elleuca, ti ringrazio per i complimenti e per le tue parole! Anche se a Napoli ci saranno ulteriori scosse sismiche di assestamento per regredire gli L1, il focus QL (QuantLotto) torna nella mia venus del cuore! Condivido il tuo pensiero in merito ai tempi maturi... frattanto non mi resta che augurare uno scintillante fine settimana

continua...

 

[Elleuca]

Buonasera Rookie. Vediamo come si comporteranno queste due sfere:

F62
G05

 

[Elleuca]

NAPOLI:

Un'immagine e' piu' eloquente di 1000 parole. Il primo tra gli L1 e' arrivato... accompagnandosi a due sfere dai sets L3... nella fascia
indicata epperoche' non e' ancora finita sotto al vesuvio. Ci saranno ulteriori scosse sismiche...di assestamento!


Vedi l'allegato 2293956

E assestamento fu!!
Lzero,Pb e due sfere da L3

 

[Rookie]

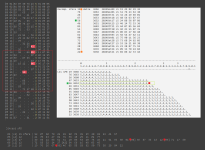
Lo scenario delle 11 venus, offre diversi spunti per le quali riflettere, ma... dal punto di vista Lotto Quantitativo (QuantLotto) , in questo momento storico e' la venus sotto il Vesuvio a essere intrigante davvero. Qui sotto e' lo scenario generale, in cui s'incastona l'anomalia temporanea, la quale dovrebbe regredire normalizzandosi velocemente:

Dunque occhio (in primis) agli LZero deinde agli LUno... ai piedi del Vesuvio. Buon vento e pale a prora.

p.s. In parole semplici, visto che gli LZero partenopei sono in forte sofferenza, dunque e' credibile che almeno 4 degli Luno provvedano alle necessita' del Caso, per regredire verso la norma di cui al calcolo teorico. A cio' si aggiunge che la situazione gia' anomala, sic stante rebus, in due estrazioni, sara' ancor piu' negativa rispetto a quanto esposto e proposto con questo post. E un occhio ai sovrappopolati sets L3 da q18 a q31

E assestamento fu!!
Lzero,Pb e due sfere da L3

NAPOLI - Un altro Splendido esempio QuantLOTTO




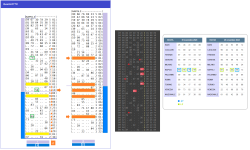
La sfida intellettuale qui esemplificata attraverso il nostro QuantLOTTO, consiste semplicemente nell'organizzare, classificare e analizzare la base di dati disponibile di stringhe di sequenze. Si tratta di qualcosa di più di un compito astratto di parsing di stringhe, perché dietro la stringa di decomposizione (o frantumazione come suole definirle il Caro @Elleuca) si nasconde l'intera complessità che discende dalla Biologia Molecolare, i cui dettami e metodi in linea di principio sono in grado di catturare una parte di questa complessità, integrando diverse fonti di informazioni in modelli probabilistici chiari, generali e trattabili per l'analisi delle sequenze.

Dobbiamo essere chiari su una cosa: il modo più affidabile per determinare la struttura o la funzione di una singola informazione all'interno della stringa è la sperimentazione diretta. Tuttavia, è molto più facile ottenere la sequenza della decomposizione di una data sfera L1 che determinare sperimentalmente la sua funzione o la sua struttura o la sua dinamica progressiva. Ciò fornisce una forte motivazione per lo sviluppo di metodi computazionali in grado di dedurre informazioni utili dalla sola sequenza.

Esempi di stringhe da analizzare:




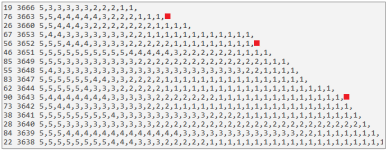
Sequenze - similarita', omologia, allineamento

La maggior parte dei problemi dell'analisi computazionale delle sequenze sono essenzialmente statistici. Le forze evolutive stocastiche agiscono su ogni successiva informazione. Individuare somiglianze significative tra sequenze divergenti in mezzo a un caos di mutazioni casuali presenta seri problemi di rapporto segnale/rumore.

Molti dei più potenti metodi di analisi disponibili fanno uso della teoria delle probabilità. Qui poniamo l'accento sull'uso di modelli probabilistici, in particolare i modelli di Markov nascosti (HMM), per fornire una struttura generale ai problemi di analisi statistica.
La natura è un'artefice e non un inventore. Le nuove sequenze vengono adattate da sequenze preesistenti piuttosto che inventate di sana pianta. Questa è una fortuna per l'analisi computazionale delle sequenze. Spesso possiamo riconoscere una somiglianza significativa tra una nuova sequenza e una sequenza di cui si sa già qualcosa; in questo modo possiamo trasferire alla nuova sequenza informazioni sulla struttura e/o sulla funzione. Diciamo che le due sequenze correlate sono omologhe e che stiamo trasferendo informazioni per omologia.

A prima vista, decidere che due sequenze sono simili non è diverso dal decidere che due stringhe di testo sono simili. Una serie di metodi per l'analisi delle sequenze è quindi radicata nell'informatica, dove esiste un'intensa letteratura sui metodi di confronto delle stringhe. Il concetto di allineamento è fondamentale. Le sequenze in evoluzione accumulano inserzioni e cancellazioni e sostituzioni, quindi prima di poter valutare la somiglianza tra due sequenze si inizia a trovare un allineamento plausibile tra di esse.

Quasi tutti i metodi di allineamento trovano l'allineamento tra due stringhe secondo uno schema di punteggio. Questi schemi di punteggio possono essere semplici come “+1 per una corrispondenza, -1 per una mancata corrispondenza”. In effetti, molti dei primi algoritmi di allineamento di sequenze erano descritti in questi termini.

Tuttavia, poiché vogliamo che lo schema di punteggio dia all'allineamento naturalmente più probabile il punteggio più alto, vogliamo tenere conto del fatto che le singole informazioni progressive degli stati successivi (nelle stringhe) hanno storie evolutive, strutture tridimensionali ripiegate e altre caratteristiche che vincolano l'evoluzione della loro sequenza primaria.

Pertanto, oltre alla matematica degli algoritmi di allineamento e confronto, il sistema di punteggio stesso richiede un'attenta riflessione e può essere complesso. Lo sviluppo di schemi di punteggio più sensibili e la valutazione dell'importanza dei punteggi di allineamento rientrano più nel campo della statistica che in quello dell'informatica. Un primo passo avanti è stata l'introduzione di matrici probabilistiche per l'assegnazione di punteggi agli allineamenti; questi servono a quantificare le preferenze evolutive per certe sostituzioni rispetto ad altre. Approcci di modellazione probabilistica più sofisticati sono stati introdotti gradualmente attraverso diverse strade. Il metodo di modellazione probabilistica ha reso possibile significativi miglioramenti predittivi, supportati da una teoria utile e coerente (teoria dei buchi), fornendo un quadro naturale in cui affrontare complessi problemi di inferenza nell'analisi computazionale delle sequenze.

 

[ciccioriccio]

In quattro parole spazio tempo forza o energia e materia se non è errato