Avevo promesso che avrei ripreso l' argomento ed eccomi ancora a trasmettervi alcune informazioni, nella speranza possano esservi utili.
Le suddivisioni delle 117.480 terzine.
2.2.2.3.5.11.89
Fra i 24 numeri, sono presenti solo l' 11 e l' 89.
Vi avevo gia' accennato, di tenere il 3 in una posizione di mezzeria o linea di demarcazione e fra un po' spieghero' meglio il perche'.
La tripletta 2.2.2 ha lo scopo di far permutare i numeri.
Se pero' cambio le posizioni, e' necessario il riconoscimento delle loro nuove sedi.
A tal punto operano 2 dei 24 numeri e cioe' l' 11 e l' 89. Solo loro hanno il potere di indicarmi le nuove posizioni che verranno generate. Nessun altro numero, ha questa particolarita' !!!!
Questa coppia non appartiene alle 10 formazioni che hanno prodotto = 1 (Ad esempio 7 e 13 oppure 11.41 e cosi' via, come gia' accennato in post precedenti).
Percio' esiste una regola di scambio, fra scala "A" e scala "B", aventi prodotto=1 (Intendendo ad esempio, per "A"=7 e per "B"=13), nella quale, per ottenere l' indice di posizione di un determinato numero, e' sufficiente moltiplicarlo per la scala opposta.
Le cose si complicano un po' se vogliamo passare da 2 tabelle che non abbiano prodotto=1.
Qui dovete armarvi di pazienza e ricavare le possibili operazioni di scambio nelle 276 combinazioni dei 24 numeri.
Vi mostrero' per ora, solo il passaggio che a noi interessa di piu', ovvero dall' 11 all' 89 e viceversa.

La 1° operazione da eseguire e' il prodotto fra 11 ed 89 : 11*89=79
La 2° operazione da eseguire ma, che e' variabile in funzione degli operandi come sopraccitato, in questo caso e' :
11+30=41 oppure (90-79)+30=41
Vi ho riportato anche alcuni esempi nei quali avendo a disposizione un numero, con questa coppia potete passare direttamente dal maggiore=89 al minore=11, semplicemente moltiplicando *41.
Il 123 degli ordinamenti, deriva proprio dalla moltiplicazione 3*41=123 ossia dalla possibilta' delle 3 permutazioni, presenti in un terno. Sono tutti gli scambi di posizione possibili ed immaginabili, disponendo di 3 numeri, con le rispettive matrici.
Un inciso : creare un quadro 90x90, con 1 sola matrice od 1 solo passo, non serve a nulla, ai fini pratici. E' solo una costruzione che genera le linee successive in ordine diametrale ma, senza alcun riscontro matematico.
La matrice richiede sempre minimo 2 assi di movimentazione, fra loro diversi.
Proseguiamo sui divisori delle 117.480 terzine : questa volta confrontiamo la parte che precede il 3 con la parte successiva.
2.2.2
5.11.89
7.13.1 Ho eseguito semplicemente le somme. verticali.
Adesso eseguo la differenza fra gli unici 2 numeri presenti, appartenenti ai 24 :
89-11=
78
Adesso sommiamo : 2+2+2=6 e 5+11+89=15
Possiamo ora unificare le 2 somme con la moltiplicazione : 6*15=
90
Possiamo ricavare il 90 con il seguente metodo : (2*5)+(2*11)+(2*89)=30 moltiplicate *3 che e' il centrale ed avrete lo stesso risultato=90.
Questo valore 90, e' di capitale importanza, per avere la possibilita' di frazionare, suddividere, filtrare l' integrale : se non fosse presente l' impresa sarebbe a dir poco, impossibile !
Vi avevo preannunciato che nei divisori delle 117.480 terzine, e' racchiusa una Tavola conosciutissima ma, poco utilizzata nei calcoli matematici.
1.7.13.78.90 appartengono al 1° quadratino della Tavola Settenaria.
Posso anche aggiungere per certo che la tabella n.3 (della serie fra le 8 fornite da Alfonso), si ricava esattamente dalla Tavola Settenaria ed a tal fine se Alfonso o Angela Martini mi leggeranno, chiedo la loro conferma.
Non ho analizzato per ora le rimanenti 7 tabelle ma, sulla 3° sono sicurissimo che l' abbiano ricavata dal modello della Tavola Settenaria.
E' stato difficile anche per me giungere a questa soluzione ma, ne e' valsa la pena.
A detta della Martini, queste tabelle sono dei potenti filtri di riduzione matematica, i migliori che possano trovarsi in rete.
La generazione di queste 8 tabelle, avviene attraverso la regola matematica delle ottave (merito ancora a Pitagora).
Passiamo ora alle 56 terzine.
I miei ragionamenti per pervenire alla soluzione corretta, sono stati questi :
il prodotto dei primi 3 divisori, abbiamo visto che sono : 2.2.2
Li ho moltiplicati, poiche' questi mi permettono la triplice permutazione : 2*2*2=8
Poi sono andato a confrontare il calcolo combinatorio in modo ascendente, cioe' partendo da 5 numeri a salire e dovevo trovare minimo 2 informazioni che andro' ad indicarvi.
Il calcolo combinatorio per il Gioco del Lotto indica quante combinazioni esistono in una serie di n numeri.

www.lottologia.com

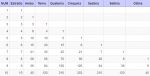
La 1° condizione che volevo trovare e' quella dell' identita' delle combinazioni fra i terni e le cinquine ed esiste : per entrambe vale 56.
La 2° condizione e' dettata dal calcolo delle ottave : se io estendo le note musicali per 7 volte, nell' 8° dovro' trovarne una che abbia il rapporto 1:2 rispetto a quella di partenza.

it.wikipedia.org
In questo caso sono tranquillo, poiche' il 56, trova la risposta della meta' per ben 2 volte, col 28 distribuito sulle combinazioni di ambi e sestine.
Per oggi vi ho detto tutto.
Alla prossima.
Ciao.