Complimenti veramente bravo, la previsione si chiude qui? saluti ArmausOttimo 17 di recupero
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Nota: This feature may not be available in some browsers.
Stai usando un browser molto obsoleto. Puoi incorrere in problemi di visualizzazione di questo e altri siti oltre che in problemi di sicurezza. .
Dovresti aggiornarlo oppure usare usarne uno alternativo, moderno e sicuro.
Dovresti aggiornarlo oppure usare usarne uno alternativo, moderno e sicuro.
TIMELINE SEQUENZA TEMPORALE
- Creatore Discussione Asuniverso
- Data di inizio
Asuniverso
Advanced Member >PLATINUM PLUS<
Se il progresso scientifico si svolgesse secondo i nostri modelli, sarebbe facile formulare idee in anticipo rispetto ai tempi. Basterebbe confrontare la scienza odierna con quella di cinquant'anni fa; tracciando geometricamente la linea di progresso, dovremmo ricavare la scienza dei prossimi cinquant'anni. Il progresso della scienza ai tempi nostri consiste nell'eliminare i congegni obsoleti con i quali le vecchie generazioni avevano formulato, e quindi spazzare via tutte quelle ragnatele.
Il fatto che possa esistere ed essere costruita una scienza come la geometria ha sempre fortemente attirato l’attenzione di tutti coloro che si interessano di fondamenti della teoria della conoscenza. Fra tutti i rami della scienza umana non ve n’è un altro che al pari di essa dia l’impressione di una Minerva saltata fuori armata di tutto punto alla testa di Giove, e di fronte alla cui potente egida il dubbio e la contraddizione abbiano così poco osato alzare gli occhi.
Ad essa non tocca in alcun modo il lungo e faticoso compito di raccogliere i fatti sperimentali, come debbono fare le scienze naturali. Propriamente dette, il nostro metodo scientifico consiste unicamente nelle deduzione. Ogni conclusione viene sviluppata da un’altra conclusione, e ciò nonostante alla fine nessuna persona di buon senso dubita che queste proposizioni geometriche non abbiano a trovare concreta applicazione nel mondo reale che ci circonda.
L’agrimensura come l’architettura, l’ingegneria meccanica come la fisica matematica calcolano continuamente relazioni spaziali dei tipi più diversi partendo dai principi della geometria; esse si attendono che i risultati delle loro costruzioni e dei loro esperimenti siano in accordo con questi calcoli e non è ancora capitato alcun caso in cui tale aspettativa sia rimasta delusa, posto che i calcoli fossero corretti e basati su dati sufficienti. La conoscenza delle connessioni casuali dei fenomeni è basata essenzialmente sulla precisione con cui noi li seguiamo queste misurazioni.
Nelle statistiche classiche, invece, dove principi semplici per tali costruzioni mancano ancora. I problemi relativi alle relazioni metriche non sono quindi problemi oziosi. Se si assume che i corpi numerici esistono indipendentemente dalla posizione, dal ritardo o dalla frequenza, la misura metrica è ovunque costante; segue quindi da misurazioni che essa deve essere diversa da quella positiva.
Il problema della validità dei postulati della geometria è connesso con il problema del fondamento interno delle relazioni metriche spaziali. In questo problema, che si può a ragione considerare proprio della filosofia dello spazio, trova applicazione l’osservazione precedente, che mentre in una varietà discreta il principio delle relazioni metriche è implicito nella nozione di questa varietà, nel caso di una varietà continua deve venire da qualche altra parte.
Quindi, o gli enti reali che sono alla base di uno spazio debbono costituire una varietà discreta, oppure il fondamento delle relazioni metriche deve essere cercato altrove, nelle forze che agiscono su di essi tenendoli assieme. Ricerche che come la presente partono da nozioni generali, possono solo aiutare a che questo compito non sia reso più difficile da concezioni anguste, e che i pregiudizi della tradizione non impediscano il progresso nella conoscenza della connessione reale delle cose.
Vedi l'allegato 2205136
Effettivamente il fatto che la geometria esista, e sia capace di tali cose, è sempre stato citato nelle controversia relativa al punto centrale di tutte le antitesi tra sistemi filosofici, come esempio vistoso della possibilità di una conoscenza di principi non poggiante su una base ricavata dall’esperienza. Inoltre la circostanza che tali principi esistono e ci si impongono è considerata una prova della tesi che lo spazio è una modalità a priori di ogni percezione esterna. Tale circostanza sembra richiedere perciò, per questa forma a priori, non semplicemente il carattere di uno schema puramente formale e di per sé privo di contenuto nel quale potrebbe adattarsi qualunque contenuto dell’esperienza: al contrario sembra attribuirle certe particolarità che fanno sì che soltanto un certo contenuto e anzi uno delimitato rigorosamente possa entrare in esso ad essere da noi percepibile.
Vedi l'allegato 2205137
Proprio questo interesse della geometria dal punto di vista della teoria della conoscenza mi incoraggia a parlare di cose matematiche a un pubblico che solo per piccolissima parte ha proceduto negli studi matematici oltre le nozioni apprese a scuola. Fortunatamente anche questo bagaglio minimo di cognizioni di geometria penso possa bastare a rendere comprensibile perlomeno il senso dei principi che intendo discutere nel seguito.
Vedi l'allegato 2205138
E’ infatti alcunché di reale gravità del corpo, o della velocità del movimento. E tali cose sono tuttavia tra loro equivalenti, se siano considerate soltanto sotto il riguardo della dimensione, come si deve fare qui e nelle discipline matematiche; appartiene infatti più ai ricercatori esaminare se il loro fondamento sia reale. Le considerazioni di questa cosa getta luce sulla geometria, poiché in essa tutti concepiscono tre specie di quantità: linea, superficie e corpo. (le tre dimensioni dei corpi numerici) qui non le facciamo oggetto di considerazione più che infinite altre. Il compito della conoscenza è quello di ricostruire la struttura dell’ente dato nel concetto, attraverso la sua correlazione con altri; ogni analisi di un concetto è la sintesi di un nuovo concetto, la ricostruzione di un ulteriore dato correlato al primo in forma necessaria. In altre parole, la conoscenza è un far valere la legge dell’oggetto nel processo del pensiero.
Vedi l'allegato 2205139
In un certo senso una teoria basata sulla deduzione è nemica della statistica sperimentale. Quest'ultima lotta continuamente per stabilire mediante prove cruciali la natura delle cose fondamentali; la prima lotta per minimizzare i successi ottenuti dimostrando quanto vasta sia la natura delle cose che può accordarsi con tutti i sistemi sperimentali.
Una teoria scientifica si mantiene valida solo finchè concorda coi fatti osservati. Se tra essa e l'osservatore permangono delle discrepanze, dopo che si è tenuto conto di tutti i possibili errori compiuti nell'osservazione stessa, allora occorre modificarla.
Milano ambata principale
6
Per recupero secondarie
17-25
Per ambo e terno anche su tutte
6-17-25
Saluti...
Non è inconcepibile che la scienza possa una volta o l'altra in futuro ideare e condurre un esperimento decisivo per risolvere la questione; tuttavia questo è un tipo di conoscenza superficiale. La teoria in oggetto può descrivere le leggi a cui la statistica innovativa obbedisce e mette in evidenza la struttura migliore; questo è in realtà il suo compito: in questo campo lascia piena libertà ai filosofi di turno, i quali dicono molto, sebbene non sembri che noi alla fine abbiamo appreso da loro qualcosa in più.

Saluti...
Ciao Asuniverso, ti devo fare davvero i complimenti, stasera a MI ambata, ambo secco a ruota e terno +3 ambi. Davvero immenso. Grazie di tutto, SrmausNon è inconcepibile che la scienza possa una volta o l'altra in futuro ideare e condurre un esperimento decisivo per risolvere la questione; tuttavia questo è un tipo di conoscenza superficiale. La teoria in oggetto può descrivere le leggi a cui la statistica innovativa obbedisce e mette in evidenza la struttura migliore; questo è in realtà il suo compito: in questo campo lascia piena libertà ai filosofi di turno, i quali dicono molto, sebbene non sembri che noi alla fine abbiamo appreso da loro qualcosa in più.
Vedi l'allegato 2205462
Saluti...
Serse
Advanced Member >GOLD<
E' il pensiero di parecchi io ho raccolto qualcosina avendo continuato con il 6.Ternooooo .....Mitico....mi sto a mangiare le mani non l ho giocato stasera pensavo avesse dato martedì.....Complimenti Asuniverso sei S.U.P.E.R.?????
Di nuovo complimenti a ASUNIVERSO.
lotto_tom75
Advanced Premium Member
Asuniverso
Advanced Member >PLATINUM PLUS<
Se il progresso scientifico si svolgesse secondo i nostri modelli, sarebbe facile formulare idee in anticipo rispetto ai tempi. Basterebbe confrontare la scienza odierna con quella di cinquant'anni fa; tracciando geometricamente la linea di progresso, dovremmo ricavare la scienza dei prossimi cinquant'anni. Il progresso della scienza ai tempi nostri consiste nell'eliminare i congegni obsoleti con i quali le vecchie generazioni avevano formulato, e quindi spazzare via tutte quelle ragnatele.
Il fatto che possa esistere ed essere costruita una scienza come la geometria ha sempre fortemente attirato l’attenzione di tutti coloro che si interessano di fondamenti della teoria della conoscenza. Fra tutti i rami della scienza umana non ve n’è un altro che al pari di essa dia l’impressione di una Minerva saltata fuori armata di tutto punto alla testa di Giove, e di fronte alla cui potente egida il dubbio e la contraddizione abbiano così poco osato alzare gli occhi.
Ad essa non tocca in alcun modo il lungo e faticoso compito di raccogliere i fatti sperimentali, come debbono fare le scienze naturali. Propriamente dette, il nostro metodo scientifico consiste unicamente nelle deduzione. Ogni conclusione viene sviluppata da un’altra conclusione, e ciò nonostante alla fine nessuna persona di buon senso dubita che queste proposizioni geometriche non abbiano a trovare concreta applicazione nel mondo reale che ci circonda.
L’agrimensura come l’architettura, l’ingegneria meccanica come la fisica matematica calcolano continuamente relazioni spaziali dei tipi più diversi partendo dai principi della geometria; esse si attendono che i risultati delle loro costruzioni e dei loro esperimenti siano in accordo con questi calcoli e non è ancora capitato alcun caso in cui tale aspettativa sia rimasta delusa, posto che i calcoli fossero corretti e basati su dati sufficienti. La conoscenza delle connessioni casuali dei fenomeni è basata essenzialmente sulla precisione con cui noi li seguiamo queste misurazioni.
Nelle statistiche classiche, invece, dove principi semplici per tali costruzioni mancano ancora. I problemi relativi alle relazioni metriche non sono quindi problemi oziosi. Se si assume che i corpi numerici esistono indipendentemente dalla posizione, dal ritardo o dalla frequenza, la misura metrica è ovunque costante; segue quindi da misurazioni che essa deve essere diversa da quella positiva.
Il problema della validità dei postulati della geometria è connesso con il problema del fondamento interno delle relazioni metriche spaziali. In questo problema, che si può a ragione considerare proprio della filosofia dello spazio, trova applicazione l’osservazione precedente, che mentre in una varietà discreta il principio delle relazioni metriche è implicito nella nozione di questa varietà, nel caso di una varietà continua deve venire da qualche altra parte.
Quindi, o gli enti reali che sono alla base di uno spazio debbono costituire una varietà discreta, oppure il fondamento delle relazioni metriche deve essere cercato altrove, nelle forze che agiscono su di essi tenendoli assieme. Ricerche che come la presente partono da nozioni generali, possono solo aiutare a che questo compito non sia reso più difficile da concezioni anguste, e che i pregiudizi della tradizione non impediscano il progresso nella conoscenza della connessione reale delle cose.
Vedi l'allegato 2205136
Effettivamente il fatto che la geometria esista, e sia capace di tali cose, è sempre stato citato nelle controversia relativa al punto centrale di tutte le antitesi tra sistemi filosofici, come esempio vistoso della possibilità di una conoscenza di principi non poggiante su una base ricavata dall’esperienza. Inoltre la circostanza che tali principi esistono e ci si impongono è considerata una prova della tesi che lo spazio è una modalità a priori di ogni percezione esterna. Tale circostanza sembra richiedere perciò, per questa forma a priori, non semplicemente il carattere di uno schema puramente formale e di per sé privo di contenuto nel quale potrebbe adattarsi qualunque contenuto dell’esperienza: al contrario sembra attribuirle certe particolarità che fanno sì che soltanto un certo contenuto e anzi uno delimitato rigorosamente possa entrare in esso ad essere da noi percepibile.
Vedi l'allegato 2205137
Proprio questo interesse della geometria dal punto di vista della teoria della conoscenza mi incoraggia a parlare di cose matematiche a un pubblico che solo per piccolissima parte ha proceduto negli studi matematici oltre le nozioni apprese a scuola. Fortunatamente anche questo bagaglio minimo di cognizioni di geometria penso possa bastare a rendere comprensibile perlomeno il senso dei principi che intendo discutere nel seguito.
Vedi l'allegato 2205138
E’ infatti alcunché di reale gravità del corpo, o della velocità del movimento. E tali cose sono tuttavia tra loro equivalenti, se siano considerate soltanto sotto il riguardo della dimensione, come si deve fare qui e nelle discipline matematiche; appartiene infatti più ai ricercatori esaminare se il loro fondamento sia reale. Le considerazioni di questa cosa getta luce sulla geometria, poiché in essa tutti concepiscono tre specie di quantità: linea, superficie e corpo. (le tre dimensioni dei corpi numerici) qui non le facciamo oggetto di considerazione più che infinite altre. Il compito della conoscenza è quello di ricostruire la struttura dell’ente dato nel concetto, attraverso la sua correlazione con altri; ogni analisi di un concetto è la sintesi di un nuovo concetto, la ricostruzione di un ulteriore dato correlato al primo in forma necessaria. In altre parole, la conoscenza è un far valere la legge dell’oggetto nel processo del pensiero.
Vedi l'allegato 2205139
In un certo senso una teoria basata sulla deduzione è nemica della statistica sperimentale. Quest'ultima lotta continuamente per stabilire mediante prove cruciali la natura delle cose fondamentali; la prima lotta per minimizzare i successi ottenuti dimostrando quanto vasta sia la natura delle cose che può accordarsi con tutti i sistemi sperimentali.
Una teoria scientifica si mantiene valida solo finchè concorda coi fatti osservati. Se tra essa e l'osservatore permangono delle discrepanze, dopo che si è tenuto conto di tutti i possibili errori compiuti nell'osservazione stessa, allora occorre modificarla.
Milano ambata principale
6
Per recupero secondarie
17-25
Per ambo e terno anche su tutte
6-17-25
Saluti...
Vi ringrazio tutti per le vostre esternazioni nei miei confronti e aggiungo: la nostra visione sul nostro modello è in gran parte dovuta alle impressioni che riceviamo attraverso i nostri sensi di aiuto artificiale, cosicché quella che chiamiamo visione basata sul senso comune, deriva in misura notevole della nostra conoscenza dei corpi numerici di dimensioni racchiuse in una gamma ristretta. Non è irragionevole dire che questo ci fornisce un’immagine dell’innovazione statistica altrettanto vicina alla realtà quanto per esempio quelle che un turista può farsi all’interno dell’Abbazia di Westminster guardando attraverso il buco della serratura di una porta laterale. Noi ricercatori innovativi per mezzo di invenzioni successive siamo riusciti ad allargare il buco della serratura, e può darsi che venga un momento in cui riusciamo a spalancare la porta. Se dunque la scienza matematica con il suo studio di corpi numerici piccolissimi e grandissimi, vicinissimi e lontanissimi, di moto e di misure molto elevate, è giunta a conclusioni che sembrano contraddire il nostro senso comune, la nostra visione sull’innovazione statistica dal buco della serratura, sembra logico considerare i suoi risultati niente più che altro dei colpi inflitti agli statisti di vecchia scuola e superati con il tempo. L’innovazione è una maga per gente fuori dal comune. Generazioni di statisti della vecchia scuola hanno cercato di penetrare i suoi segreti: ma pezzo per pezzo il travestimento viene strappato via, ma sembra che ogni scoperta serva a mettere in luce nuove vie statistiche da esplorare. L’innovazione statistica è una vera donna è avrà l’ultima parola. I ricercatori statistici di ogni epoca possono far eco alle nostre parole riferenti al nostro lavoro di tutta una vita. Non so come io posso apparire a voi, ma per quanto mi riguarda mi sembra di essere stato soltanto un bambino che giuoca sulla spiaggia ed è contento quando trova un ciottolo più levigato o una conchiglia più graziosa del solito, mentre il grande mare della verità è davanti a lui ancora tutto da scoprire.
Saluti…
Ultima modifica:
Coccobello
Advanced Member >PLATINUM<
È la prima volta che la seguo, ho visto che ha preso un terno, complimenti per la sua bravura e competenza, non le chiedo di regalare ancora una splendida vincita, perché un terno nn è cosa da poco, ma se ci sono le condizioni ci faccia ancora sognare, magari con un piccolo ambo che può far felici tante persone! Grazie!!!
Asuniverso
Advanced Member >PLATINUM PLUS<
La teoria della separazione misurata lungo la linea degli eventi senza matematica è come il lavorare senza fatica o lo sciare senza cadere o l’estrazione indolore dei denti. L’affermazione può spaventare, ma la matematica che noi usiamo è una matematica alla portata di chiunque , con un minimo di preparazione che si è detto, voglia affrontare i temi di fondo di una branca innovativa del sapere che è tra le componenti principali del modo statistico contemporaneo. Certamente un’esposizione eccezionale per densità di idee, rigore concettuale e chiarezza di linguaggio anche al lettore meno esperto. Le esigenze critiche di un pubblico non più alle prime armi hanno visto un netto progresso della letteratura divulgativa ed epistemologica.
Mi si permetta a questo proposito una riflessione un po’ estranea all’argomento che sto trattando. Alcuni anni or sono un filosofo disse che mentre il futuro è determinato dal passato, il passato non è dal futuro o, in altri termini, che dalla conoscenza del presente possiamo inferire quella del futuro, ma non quella del passato. A suo dire, ciò dipendeva dal fatto che una causa produce un unico effetto, mentre uno stesso effetto può essere prodotto da più cause. E’ chiaro che nessuno statista potrà sottoscrivere questa asserzione: le leggi della natura connettono l’antecedente al conseguente in modo tale che l’antecedente è determinato dal conseguente così come il conseguente dall’antecedente. Ma quale può essere stata l’origine dell’errore di quel filosofo? Sappiamo che, in virtù del principio di Carnot, i fenomeni fisici sono irreversibili e che la statistica tende verso l’uniformità.
Quando cerchiamo di prevedere un fatto e ne esaminiamo gli antecedenti, ci sforziamo di acquisire informazioni sulla situazione anteriore: ma non saremo in grado di farlo per tutte le parti esaminate, e ci contentiamo di sapere ciò che accade nelle vicinanze del punto in cui il fatto deve verificarsi, o ciò che sembra avere un qualche rapporto con il fatto in questione. Un’indagine non può mai essere completa e bisogna saper scegliere. Ma ci può succedere di aver trascurato delle circostanze che a prima vista ci sembrano del tutto estranee al fatto previsto, alle quali non avremmo mai pensato di attribuire alcuna influenza e che invece, al contrario di ogni previsione, si trovano a svolgere un ruolo decisivo.
Un uomo cammina per strada andandosene a sbrigare i propri affari: qualcuno, che fosse al corrente di questi suoi affari, potrebbe dire per quale ragione egli è uscito a quell’ora, perché è passato per quella strada. Su un tetto lavora un muratore: l’imprenditore che lo ha alle proprie dipendenze potrà prevedere in una certa misura ciò che egli farà. Ma l’uomo non pensa affatto al muratore, né quest’ultimo all’uomo; essi sembrano appartenere a due mondi completamente estranei l’uno dall’altro. E tuttavia il muratore lascia cadere una tegola che uccide l’uomo, e non esiteremo a dire che il tutto è opera del caso.
La nostra debolezza non ci permette di abbracciare tutto l’universo e ci obbliga a tagliarlo a fette. Cerchiamo di farlo nel modo meno artificioso possibile: ciò nondimeno, di tanto in tanto, succede che due di queste fette abbiano delle ripercussioni l’uno sull’altra. Gli effetti di questa azione reciproca ci paiano allora dovuti al caso. E’ questo un terzo modo di concepire il caso? Non sempre: effettivamente, il più delle volte si è ricondotti alla prima o alla seconda concezione. Quando due mondi, generalmente estranei l’uno all’altro, vengono a integrare tra di loro, le leggi di questa interazione non possono che essere molto complesse, e d’altra parte sarebbe stato sufficiente un piccolissimo cambiamento nelle condizioni iniziali per impedire che essa avesse luogo. Sarebbe bastato davvero poco perché l’uomo passasse un secondo più tardi o il muratore lasciasse cadere la tegola un secondo prima!
Tutto ciò che abbiamo detto non spiega ancora perché il caso obbedisca a certe leggi. E’ sufficiente che le cause piccole o che esse siano complesse per potere prevedere quali effetti avranno, se non in ogni singolo caso, quantomeno in media? Ciò spiega perché i fenomeni obbediscano alle leggi del caso quando piccole differenze nelle cause sono sufficienti a produrre grandi differenze negli effetti. Le probabilità di queste piccole differenze si possono infatti considerare proporzionali alle differenze stesse, appunto perché tali differenze sono piccole e i piccoli incrementi di una funzione continua sono proporzionali a quella della variabile.
Ma i paradossi non sono ancora finiti. La finzione immaginaria da Flammarion, quella dell’uomo che va più veloce della luce e per quale il tempo ha cambiato di segno. Diciamo che per costui tutti i fenomeni sembrerebbero dovuti al caso. Ciò è vero da un certo punto di vista; nondimeno, tutti questi fenomeni a un dato istante non sarebbero distribuiti secondo le leggi del caso, giacché sarebbero distribuiti coma appaiono a noi che, vedendoli svolgersi in modo armonioso e senza scaturire da un caos primigenio, non li consideriamo come governati dal caso.
Supponiamo che nello spazio di C e D un corpo numerico parta da C e si diriga con velocità costante verso D, percorrendo, secondo C, la distanza CD = 78/90
e di conseguenza:
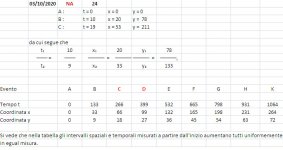
Quindi:


da cui si ricava

e successivamente
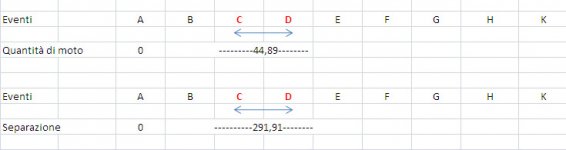
Questa relazione mostra come la lunghezza di CD si possa calcolare conoscendo gli intervalli spaziali tra A e K , i quali si ottengono, come prima, con una equazione, se sono note le coordinate di C e D.
Napoli ambata principale
24
Per recupero secondarie
66-57
Per ambo e terno anche su tutte
24-66-57
Saluti...
Mi si permetta a questo proposito una riflessione un po’ estranea all’argomento che sto trattando. Alcuni anni or sono un filosofo disse che mentre il futuro è determinato dal passato, il passato non è dal futuro o, in altri termini, che dalla conoscenza del presente possiamo inferire quella del futuro, ma non quella del passato. A suo dire, ciò dipendeva dal fatto che una causa produce un unico effetto, mentre uno stesso effetto può essere prodotto da più cause. E’ chiaro che nessuno statista potrà sottoscrivere questa asserzione: le leggi della natura connettono l’antecedente al conseguente in modo tale che l’antecedente è determinato dal conseguente così come il conseguente dall’antecedente. Ma quale può essere stata l’origine dell’errore di quel filosofo? Sappiamo che, in virtù del principio di Carnot, i fenomeni fisici sono irreversibili e che la statistica tende verso l’uniformità.
Quando cerchiamo di prevedere un fatto e ne esaminiamo gli antecedenti, ci sforziamo di acquisire informazioni sulla situazione anteriore: ma non saremo in grado di farlo per tutte le parti esaminate, e ci contentiamo di sapere ciò che accade nelle vicinanze del punto in cui il fatto deve verificarsi, o ciò che sembra avere un qualche rapporto con il fatto in questione. Un’indagine non può mai essere completa e bisogna saper scegliere. Ma ci può succedere di aver trascurato delle circostanze che a prima vista ci sembrano del tutto estranee al fatto previsto, alle quali non avremmo mai pensato di attribuire alcuna influenza e che invece, al contrario di ogni previsione, si trovano a svolgere un ruolo decisivo.
Un uomo cammina per strada andandosene a sbrigare i propri affari: qualcuno, che fosse al corrente di questi suoi affari, potrebbe dire per quale ragione egli è uscito a quell’ora, perché è passato per quella strada. Su un tetto lavora un muratore: l’imprenditore che lo ha alle proprie dipendenze potrà prevedere in una certa misura ciò che egli farà. Ma l’uomo non pensa affatto al muratore, né quest’ultimo all’uomo; essi sembrano appartenere a due mondi completamente estranei l’uno dall’altro. E tuttavia il muratore lascia cadere una tegola che uccide l’uomo, e non esiteremo a dire che il tutto è opera del caso.
La nostra debolezza non ci permette di abbracciare tutto l’universo e ci obbliga a tagliarlo a fette. Cerchiamo di farlo nel modo meno artificioso possibile: ciò nondimeno, di tanto in tanto, succede che due di queste fette abbiano delle ripercussioni l’uno sull’altra. Gli effetti di questa azione reciproca ci paiano allora dovuti al caso. E’ questo un terzo modo di concepire il caso? Non sempre: effettivamente, il più delle volte si è ricondotti alla prima o alla seconda concezione. Quando due mondi, generalmente estranei l’uno all’altro, vengono a integrare tra di loro, le leggi di questa interazione non possono che essere molto complesse, e d’altra parte sarebbe stato sufficiente un piccolissimo cambiamento nelle condizioni iniziali per impedire che essa avesse luogo. Sarebbe bastato davvero poco perché l’uomo passasse un secondo più tardi o il muratore lasciasse cadere la tegola un secondo prima!
Tutto ciò che abbiamo detto non spiega ancora perché il caso obbedisca a certe leggi. E’ sufficiente che le cause piccole o che esse siano complesse per potere prevedere quali effetti avranno, se non in ogni singolo caso, quantomeno in media? Ciò spiega perché i fenomeni obbediscano alle leggi del caso quando piccole differenze nelle cause sono sufficienti a produrre grandi differenze negli effetti. Le probabilità di queste piccole differenze si possono infatti considerare proporzionali alle differenze stesse, appunto perché tali differenze sono piccole e i piccoli incrementi di una funzione continua sono proporzionali a quella della variabile.
Ma i paradossi non sono ancora finiti. La finzione immaginaria da Flammarion, quella dell’uomo che va più veloce della luce e per quale il tempo ha cambiato di segno. Diciamo che per costui tutti i fenomeni sembrerebbero dovuti al caso. Ciò è vero da un certo punto di vista; nondimeno, tutti questi fenomeni a un dato istante non sarebbero distribuiti secondo le leggi del caso, giacché sarebbero distribuiti coma appaiono a noi che, vedendoli svolgersi in modo armonioso e senza scaturire da un caos primigenio, non li consideriamo come governati dal caso.
Supponiamo che nello spazio di C e D un corpo numerico parta da C e si diriga con velocità costante verso D, percorrendo, secondo C, la distanza CD = 78/90
e di conseguenza:

Quindi:


da cui si ricava

e successivamente

Questa relazione mostra come la lunghezza di CD si possa calcolare conoscendo gli intervalli spaziali tra A e K , i quali si ottengono, come prima, con una equazione, se sono note le coordinate di C e D.
Napoli ambata principale
24
Per recupero secondarie
66-57
Per ambo e terno anche su tutte
24-66-57
Saluti...
Ultima modifica:
Ultima estrazione Lotto
-
Estrazione del lotto
sabato 07 marzo 2026Bari7221493107Cagliari2811570385Firenze4176270179Genova7619374069Milano1823562157Napoli1089633148Palermo3915857714Roma9051568916Torino1004730661Venezia8970466156Nazionale3137896468Estrazione Simbolotto
Firenze



 2943320825
2943320825