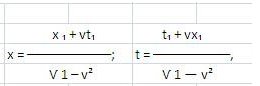TIMELINE SEQUENZA TEMPORALE

[Asuniverso]

Scusa Ciccio90 ma ai riportato una cosa sbagliata ,io o proposto 16 61 al primo colpo a na 61 .la cosa che ai tu ai postato e la elaborazione fatta da Asuniverso che deve ancora uscire , chiedo alla direzione se si possono togliere i miei post da questo blog di Asuniverso scusandomi con lui di questa mia intrusione nel suo blog ti59

ti59 non devi chiedere nessuna scusa e non devi cancellare nessun post, in questa pagina sono tutti ben voluti, non ti ho risposto, ma ti risponderò il più breve possibile al tuo quesito, ciao.

 

[Asuniverso]

mi scuso con Asuniverso per scrivere sul suo blog ,al secondo colpo na 61 potrebbe ancora uscire il 16 ,se vuole riprovare 83 38 ba mi na ve grazie ti59

ti59 per il tuo 16 mi piace su Bari in abbinamento con il 83-38, mentre sulle restanti ruote puoi benissimo giocare solo per ambo, ciao.

 

[ti59]

Grazie Asuniverso vediamo cosa esce ti59

 

[Asuniverso]

Abbiamo tratto indizi dal mondo reale. Spesso gli indizi ci sono venuti da aree del tutto diverse da quelle della loro applicazione finale. Anche se tutto quello che facciamo è trarre conclusioni logiche da assunti iniziali. La nostra indagine svolge sulle dieci ruote, ed analizziamo tutti i novanta corpi numerici che vanno a formare le 1.174.800 terzine. Dalle nostre osservazioni che è emerso finora, è che, quando un sistema di corpi numerici è sottoposto a maggiori sollecitazioni, gli stati osservati perdono velocità e guadagnano complessità sia spaziale sia temporale.

Questo stato di caratteristiche permette infatti di discernere in esso imperfezioni che ne rendono la struttura distinguibile. Quel che troviamo è uno stato che in un certo senso sembra presentare, al meno in media, meno velocità dello stato da cui è emerso. La maggior parte delle regolarità che abbiamo descritto si formano attraverso perdite di misure. Il corpo si divide, perde misura e guadagna meno velocità. Pare ragionevole chiederci quale effetto le misure, gli intervalli, la velocità abbiano sulla dinamica caotica. Tutto questo può coesistere col caos o regolarità? I due termini sembrano contraddittori. Eppure la risposta è sì e conduce ad un argomento che merita di essere esplorato per il suo interesse.

Ci proponiamo ora di fornire una rapida introduzione all’argomento descritto. Supponiamo di voler costruire un modello di come le 1.174.800 terzine variano nella loro dinamica. Ma quale regola dovremmo scegliere? Una scelta allettante è un’equazione. Ci riferiamo alla cosiddetta equazione di intervallo tra gli eventi.

La formula in questione è:


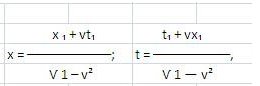
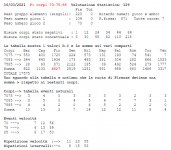
Diamo qui di seguito il risultato della nostra indagine svolta sulle dieci ruote, con l'analisi di 1.174.800 terzine. Le ricerche su cui abbiamo appena riferito sembrano preferire la ruota di Firenze (facoltativa Nazionale), la quale pone una sola varietà dinamica superiore.


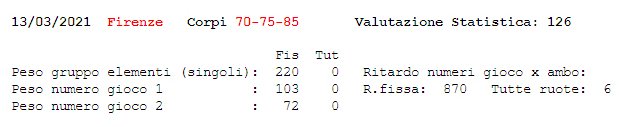
Esaminiamo attentamente la sequenza delle misure corpi stato potenziale. La misura non è compatibile; se si osserva in dettaglio lo stato della sequenza misure corpi stato concettuale, si possono infatti discernere delle imperfezioni che ne rendono la struttura distinguibile. Quel che troviamo è uno stato che in un certo senso sembra presentare una differenza di misura.
Misure corpi stato potenziale ----1-12-24-34-44-83
Misure corpi stato concettuale --1-12-24-36-48-90
Attualmente questa è una spiegazione certa di ciò che accade in queste due strutture di misure incompatibili.

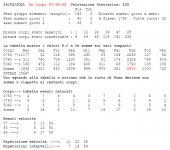
Ripetendo il processo descritto, ma cominciando con la serie dei valori negativi, gli iterati possono scendere di misura al di sotto del loro valore potenziale, mentre l’insieme dei corpi positivi deve rimanere stabile (non deve avvenire nessuna variazione di misura).
Intervalli corpi stato negativi---3-30-58---82-113-218
Intervalli corpi stato positivi ---1-36-72-108-144-270
Avendo in mente questo esempio, possiamo trovare gruppi di strutture negative molto interessanti con il confronto dei positivi.



Questa sequenza degli eventi della velocità ha un’interpretazione di confronto nei termini degli attrattori associati, la quale viene restituita attraverso una serie di traiettorie che perdono velocità da quelle iniziale.

La ripetizioni di velocità e degli intervalli si muovono in uno spazio verso il quale i corpi ruotano in un sistema dinamico dove le traiettorie che arrivano ad esse devono raggiungere uno stato sottoposto a maggiori sollecitazioni.

Le equazioni semplificate ci dicono quali di questi possibili fenomeni si verifichino realmente; ma è utile sistematizzare gli effetti generali della velocità e sviluppare modelli teorici per trattarli. L'idea è quella di distinguere in anticipo fra ciò che ci si deve attendere e ciò che è sorprendente.

Saluti...

 

[Ciccio90]

CIAO ASUNIVERSO.
PROVERO A LEGGERE, MA SONO SICURO CHE NON RIUSCIRO.
COMUNQUE GRAZIE.
COMPLIMENTI PER LA TUA PREPARAZIONE, I TUOI STUDI.
CIAO. BUONA SERATA.

 

[Asuniverso]

CIAO ASUNIVERSO.
PROVERO A LEGGERE, MA SONO SICURO CHE NON RIUSCIRO.
COMUNQUE GRAZIE.
COMPLIMENTI PER LA TUA PREPARAZIONE, I TUOI STUDI.
CIAO. BUONA SERATA.

Ciccio90 ti ringrazio per i complimenti, ma ricordati che per correre bisogna prima iniziare a camminare. Mi avevi chiesto un pronostico e ti ho esaudito, ciao.

 

[Ciccio90]

PROVERO COME AMBATE ED AMBO.
GRAZIE ASUNIVRSO

 

[Asuniverso]

Di solito per il ricavo dei nostri pronostici l’abbiamo sempre rappresentato con delle equazioni matematiche, ma questo fatto non spiega però lo strano modo in cui la matematica sembra amplificare le nostre percezioni. Da un lato noi sembriamo ricavare da una teoria matematica più di quel che vi abbiamo messo, anche se tutto quel che facciamo è trarre conclusioni logiche da assunti iniziali.

Ovviamente molte di queste conclusioni non sono inizialmente così ovvie, come sa bene chiunque abbia studiato matematica superiore. D’altro canto la matematica ci costringe a sapere ciò che deve seguire dai nostri assunti. L’osservazione apparentemente semplice che gli stessi assunti implicano le stesse conclusioni è un’osservazione di grande importanza e aiuta a spiegare perché la matematica ci regali più di quanto noi le formiamo.

Questa appendice fornisce le formule necessarie per tracciare i nostri pronostici. La progettazione segue le stesse linee elencate qui sotto.

Vedi l'allegato 2211518
Vedi l'allegato 2211519
Vedi l'allegato 2211523
Diamo qui di seguito il risultato della nostra indagine svolta sulle 11 ruote, con l'analisi di 1.292.280 terzine. Le ricerche su cui abbiamo appena riferito sembrano preferire la ruota di Genova, la quale pone una varietà di questioni dinamiche superiori.
Vedi l'allegato 2211541

Vedi l'allegato 2211526

Vedi l'allegato 2211532

Vedi l'allegato 2211528

Vedi l'allegato 2211529
Le equazioni semplificate ci dicono quali di questi possibili fenomeni si verifichino realmente; ma è utile sistematizzare gli effetti generali della velocità e sviluppare modelli teorici per trattarli. L'idea è quella di distinguere in anticipo fra ciò che ci si deve attendere e ciò che è sorprendente.

Saluti...

Quando ci si trova a dover affrontare una situazione complicata, spesso la cosa migliore è quella di porsi a cercare di risolvere i problemi, giusto per avere un'idea della direzione nella quale si sta andando. C'è una ben sviluppata teoria matematica della dinamica complessa per la ricerca dell'ambo, e con l'estrazione del 16/03/2021 abbiamo avuto conferma sull'evolversi dei nostro modello.




Saluti...

 

[Rookie]

Quando ci si trova a dover affrontare una situazione complicata, spesso la cosa migliore è quella di porsi a cercare di risolvere i problemi, giusto per avere un'idea della direzione nella quale si sta andando. C'è una ben sviluppata teoria matematica della dinamica complessa per la ricerca dell'ambo, e con l'estrazione del 16/03/2021 abbiamo avuto conferma sull'evolversi dei nostro modello.

Vedi l'allegato 2211895
Vedi l'allegato 2211897

Saluti...

Complimentissimi Asuniverso! Ad majora...

 

[Elleuca]

Complimentissimi Asuniverso

 

[Ciccio90]

Quando ci si trova a dover affrontare una situazione complicata, spesso la cosa migliore è quella di porsi a cercare di risolvere i problemi, giusto per avere un'idea della direzione nella quale si sta andando. C'è una ben sviluppata teoria matematica della dinamica complessa per la ricerca dell'ambo, e con l'estrazione del 16/03/2021 abbiamo avuto conferma sull'evolversi dei nostro modello.

Vedi l'allegato 2211895
Vedi l'allegato 2211897

Saluti...

BRAVO ASUNIVERSO. GRANDE.

 

[ti59]

Solo 83 a ve ti59

 

[Asuniverso]

Solo 83 a ve ti59

Si ho notato, ti59, se puoi ti consiglio di portare avanti il mio pronostico su Firenze 70-75-85 (facoltativo Nazionale e tutte) ciao buona giornata.

 

[ti59]

Grazie Asuniverso per il tuo suggerimento . se ai tempo mi potresti elaborare 26 62 ba mi na ve grazie ti59

 

[.MRK1.]

ciao, ho visto 70 75 85 fi

bello il num 85

ciao sempre bravo , studi stupendi ,,,

 

[Asuniverso]

Grazie Asuniverso per il tuo suggerimento . se ai tempo mi potresti elaborare 26 62 ba mi na ve grazie ti59

ti59 in rosso la ruota dove mi piace il tuo pronostico, ciao.

 

[Asuniverso]

ciao, ho visto 70 75 85 fi

bello il num 85

ciao sempre bravo , studi stupendi ,,,

Grazie M.R.K1, 85 ottimo!!! Ciao

 

[Asuniverso]

Aggiornamento tabella del 16/03/2021 "Corpi numerici velocità"

La tabella che stiamo per descrivere è usata per far luce sul problema generale della formazione di tipi di movimento dei corpi numerici. Quest’aria molto studiata è la conversione per ambo, che abbiamo esposto nei post precedenti, in connessione con la formazione delle ambate. La nostra indagine svolge sulle dieci ruote, ed analizziamo tutti i novanta corpi numerici che vanno a formare le 1.174.800 terzine. Dalle nostre osservazioni che è emerso finora, è che, quando un sistema di corpi numerici è sottoposto a maggiori sollecitazioni, gli stati osservati perdono velocità e guadagnano complessità sia spaziale sia temporale.


<------------------------------------------------------------------------------------------------------------------------------------------------->

<------------------------------------------------------------------------------------------------------------------------------------------------->


Le equazioni semplificate ci dicono quali di questi possibili fenomeni si verifichino realmente; ma è utile sistematizzare gli effetti generali della velocità e sviluppare modelli teorici per trattarli. L'idea è quella di distinguere in anticipo fra ciò che ci si deve attendere e ciò che è sorprendente.

Saluti…

 

[ti59]

Grazie Asuniverso per la elaborazione vediamo cosa esce ti59

 

[Asuniverso]

Grazie Asuniverso per la elaborazione vediamo cosa esce ti59

Auguriamo in bene, ciao ti59