Per dimensioni non intendiamo altro che la misura e la norma secondo cui un corpo numerico è considerato misurabile: in maniera che non soltanto la lunghezza sono dimensioni del corpo, ma anche la dimensione secondo cui i numeri sono pesanti, la velocità è la dimensione del movimento, e così via all'infinito. Poiché la stessa divisione in più parti uguali, o che sia reale, o che sia soltanto mentale, è propriamente la dimensione secondo la quale numeriamo i corpi; e in quel modo che costituisce il numero, si dice propriamente che è una forma di dimensioni, quantunque ci sia qualche diversità nel significato della parola. Se infatti consideriamo le parti in ordine al tutto, allora diciamo di numerare; se al contrario riguardiamo il tutto come diviso in parti, lo misuriamo.
Questo sviluppo, appena schematizzato, delle teorie matematiche essenziali per la formulazione della separazione lungo una linea degli eventi ha apportato dapprima a considerare la metrica dei corpi numerici come il concetto fondamentale sul quale si basa il modello. Partendo da questo concetto, presenteremo in successione la teoria, evitando di trattare argomenti che non sono necessari al nostro scopo.
Il corpo in questione 21-16-23 che viaggia sulla ruota di Roma come un corpo unico in linea
A e
F
Vedi l'allegato 2247152
Vedi l'allegato 2247153
Vedi l'allegato 2247154
Ciò che si misura è la massa estrattiva, rapporto la cui intensità diminuisce in proporzione della stessa distanza estrattiva.
Vedi l'allegato 2247158
E’ chiaro che questo valore
396 è una forza di carattere completamente diverso, che non agisce per mezzo di un contatto diretto, ma sembra un influsso che si irradia attraverso lo spazio della locazione della massa estrattiva e la cui intensità diminuisce in ragione inversamente proporzionale della stessa distanza estrattiva.
Vedi l'allegato 2247159
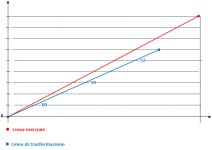
Questa relazione mostra che, in termini di distanze o intervalli spaziali, malgrado valori diversi, hanno le stesse proprietà fisiche i due valori.
Questo rapporto mostra come la lunghezza si possa calcolare conoscendo gli intervalli temporali dei sistemi inerziali e dai sistemi di trasformazione di spostamento, i quali si ottengono, con una sottrazione, se sono note le coordinate di
A-B + A-
C + A-
F
Vedi l'allegato 2247162
Gli intervalli temporali dei sistemi inerziali e dai sistemi di trasformazione di spostamento, si ottengono, con una sottrazione, se sono note le coordinate di
A-B + A-
C + A-
F
Vedi l'allegato 2247163
= differenza intervallo temporale
2833339
Vedi l'allegato 2247164
Vedi l'allegato 2247165
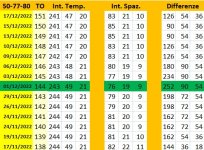
La tabella mostra che, la locazione spaziale estrattiva della numero 139, sulla ruota di Roma produce una grandezza crescente del punteggio e di conseguenza un aumento anche della dimensione.
Vedi l'allegato 2247166
Questa turbolenza di moto estrazionale che si verifica offre di determinare i particolari fini, come per esempio quali tipi di diversità accadono nei corpi numerici: il fenomeno della contrazione, delle posizione, o della velocità che esercita l’attrazione nell'istante in cui esso parte. Le coordinate dei nostri punti materiali dovranno dunque soddisfare a certe equazioni dette vincolari. Soltanto allora le differenze dei valori decimali che abbiamo posto in evidenza diventano percepibili. Ciascuna delle misure che individuano e determinano l’estensione di un corpo numerico (corpo di tre elementi che viaggia come un corpo unico) sia in altezza che in lunghezza vengono associati i termini punteggio e dimensioni.
In altre parole, il punteggio maggiore di un corpo numerico prodotto dalla forza della dimensione dipende unicamente dalla sua posizione nello spazio, e non dalla forma, composizione e massa del corpo. L’accelerazione di un corpo numerico è cioè misurata dall’aumento di punteggio in un intervallo unitario di dimensione. Se il punteggio aumenta, l’accelerazione è positiva, viceversa è negativa. Nel nostro caso è positiva, vediamo che aumenta da 192 a 220.