La teoria delle linee è strettamente connessa con la teoria dello spazio e del tempo. Inizierò quindi con una breve analisi dell’origine delle nostre idee sullo spazio e sul tempo,
anche se mi rendo conto che, così facendo, mi addentro in un terreno controverso. Il nostro modello è il tentativo di coordinare le nostre esperienze e di organizzarle in un sistema logico. Ma in che modo le nostre abituali idee di spazio e di tempo sono legate al carattere delle nostre esperienze? Le esperienze individuali ci appaiono organizzate in modo tale che i singoli eventi che si è in grado di ricordare sembrano ordinate secondo il criterio del prima e del dopo. Naturalmente, è possibile associare agli eventi dei numeri, per esempio associare a un evento remoto un numero maggiore di quello associato a un evento recente. Per esempio, si può definire questa associazione mediante una funzione di misura, cioè confrontando l’ordine degli eventi fornito dalla misura con l’ordine della successione di altri eventi. Per misura intendiamo qualcosa che fornisce una serie di eventi misurabili, ma che ha anche altre proprietà di cui parleremo in seguito.
La sola giustificazione dei nostri concetti e dei nostri sistemi di concetti è il fatto che essi servono a rappresentare l’insieme delle nostre esperienze;
Sono convinto che i filosofi hanno sempre avuto un effetto d’annoso sul progresso del pensiero innovativo poiché hanno sottratto molti concetti fondamentali al dominio dell’empirismo.
Veniamo adesso alle nostre concezioni sullo spazio numerico.
SPAZIO E TEMPO
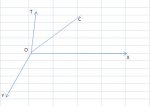
Le linee possono ovviamente avere una forma qualsiasi; una volta precisato l'osservatore, la forma è un indice della storia del corpo numerico. Che cosa può significare il fatto che una linea di frequenza sia retta?
Scegliamo l'origine O in maniera che il corpo numerico sia presente in tale punto all'ora zero e sortisce in P,
punto di coordinate x₁ e y₁, t₁.
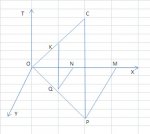
Si traccino il segmento PC, lungo t₁ unità, parallelamente all'asse dei tempi e il segmento PM perpendicolare a OX in modo che sia OM = x₁, MP = y₁.
I punti O e C rappresentano allora nello spazio tempo la frequenza e l'evento del corpo numerico, la cui linea di moto supporremo sia la retta OC. Sia K un punto qualsiasi di OC rappresentante un evento dell'evolversi del corpo numerico e siano x, y e t le sue coordinate; nella figura sottostante si ha ON = x, NQ = y OK = t.
Queste coordinate sono la misura degli intervalli spaziali e dell'intervallo temporale a partire dalla formulazione dei corpi di Milano.
Vedi l'allegato 2202881
Vedi l'allegato 2202882
Ciò significa che tanto gli intervalli temporali quanto quelli spaziali, misurati a partire dall'evento dell'evolversi del corpo numerico, aumentano uniformemente in ugual misura, e ne segue anche che la stessa separazione tra un evento aumenta uniformemente nella stessa misura.
Un esempio numerico può rendere più comprensibili questi concetti.
Supponiamo che lo sviluppo del moto del corpo numerico sia rappresentato dalla seguente tabella, in cui le unità di tempo e di spazio sono rispettivamente:
Vedi l'allegato 2202883
Vedi l'allegato 2202884
Si vede che nella tabella gli intervalli spaziali e temporali misurati a partire dall'inizio aumentano tutti uniformemente in egual misura.
Prendiamo per esempio, l'intervallo tra gli eventi
D e
E.
Vedi l'allegato 2202885
Vedi l'allegato 2202889
Considerati da un punto di vista logico, essi sono libere creazioni dell'intelletto umano, strumenti del pensiero, che debbono servire allo scopo di porre le esperienze in relazione l'una con l'altra, e di poterle quindi abbracciare meglio con lo sguardo. Il tentativo di rendersi conto delle fonti empiriche di questi concetti fondamentale deve mostrare in quale misura noi siamo effettivamente legati a questi innovativi concetti. In tal modo diventiamo coscienti della nostra libertà, libertà di cui, in caso di necessità, riesce sempre difficile fare un uso ragionevole.
Milano ambata principale
25
Per recupero secondarie
08-06
Per ambo e terno anche su tutte e Nazionale
25-08-06
Saluti...
 All'epoca,correggimi se sbaglio, utilizzavi dei metodi sommativi, ora è matematica ad alti livelli che probabilmente pochi riescono a seguire, compreso il sottoscritto. Per seguire si sarebbe dovuto studiare parecchio in materia. Però se questa metodologia da buoni risultati, chi ti segue, anche senza comprendere, potrebbe utilizzare le sole previsioni che è già un bel fare.
All'epoca,correggimi se sbaglio, utilizzavi dei metodi sommativi, ora è matematica ad alti livelli che probabilmente pochi riescono a seguire, compreso il sottoscritto. Per seguire si sarebbe dovuto studiare parecchio in materia. Però se questa metodologia da buoni risultati, chi ti segue, anche senza comprendere, potrebbe utilizzare le sole previsioni che è già un bel fare.