E’ venuto il momento di riprendere un tema che abbiamo lasciato in sospeso nella discussione dell’esperimento della massa di estrazione. Questo stato di massa estrazionale è una vera sorpresa: questa massa d’estrazioni, esibisce un comportamento altamente distintivo, lo stesso comportamento che appare in quel moto molto più semplice. Questo tipo di formazione di regolarità estrazionale ha una propria regola: si guadagna struttura della perdità di misura del moto estrattivo. In effetti il quadro generale che è emerso finora è che, quando un sistema è sottoposto a maggiori sollecitazioni, gli stati osservati perdono velocità e guadagnano complessità sia spaziale sia temporale. Quel che troviamo è uno stato che in un certo senso sembra presentare, almeno in media, meno velocità da cui è emerso. Attualmente non esiste alcuna spiegazione certa di ciò che accade in questa forma di creazione di misura. Così siamo ricondotti alla nostra intuizione abituale: l’immaginazione umana da sola di fronte all’infinito.
Quando ci si trova a dover affrontare una situazione complicata, spesso la cosa migliore è quella di porsi a cercare di risolvere i problemi più semplici possibili, giusto per avere un’idea della direzione nella quale si sta andando. C’è una bella teoria matematica della dinamica complessa, la teoria del caos, a cui è dedicato il modello. Non c’è dubbio che il moto turbolento sia complicato, almeno quanto la dinamica caotica. Secondo la teoria prevalente, in effetti, la turbolenza della massa estrazionale sarebbe una manifestazione fisica della dinamica estrazionale. Essendo impossibile studiare direttamente l’effetto caotico, pare ragionevole chiedersi quale effetto la massa estrazionale 0,0097199805600389 produce sulla dinamica caotica.
I due termini sembrano contradditori. Eppure la risposta è si, e conduce a un argomento che merita di essere esplorato per il suo interesse intrinseco. Per usare questo modello, prendiamo una massa estrazionale iniziale 0,0097199805600389
Non dobbiamo accontentarci di cosa succede in quella parte A-F, ma dobbiamo anche sapere cosa accade nelle vicinanze del punto della massa estrazionale 0,0097199805600389.
Ci chiediamo quindi: quali sono le simmetrie del sistema per conseguire una numerica più completa. Nella misura del possibile introdurremo le misure dettagliate del modello.
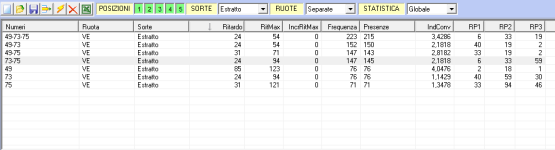
La posizione estrattiva della numero 104, produce il seguente scostamento sulla ruota di Venezia:
Si evidenzia nello schema delle due grafiche, che quando si attiva un sistema dato, può essere stabile inizialmente al massimo uno di questi due tipi, ma può anche non esserlo nessuno. L’alternativa è però che abbiamo tre diversi tipi di sfasamento A-B, A-C, A-F Dal punto di vista della teoria, questo strano risultato emerge in modo naturale e inevitabile, ed è pienamente confermato da esperimenti compiuti.
Non appena appare un mutamento lungo le varie simmetrie temporali della linea
A-
F, la simmetria temporale si trasforma in stati diversi. Dapprima esso si trovava in uno stato stazionario e non fa niente; ma al mutare della variabile esterna si sviluppa una lievissima diversità di scostamento, il quale poi cresce fino a diventare pronunciata. L’intero processo viene turbato per effetto degli spostamenti estrattivi, ciò significa che lo spostamento estrattivo produce versione con fasi spostate lungo tutta la superficie della linea temporale
A-
F. Le date inerenti alla massa estrazionale sono convenzioni umane e a parità di tutto il resto il risultato di un esperimento non dipende dal giorno della settimana in cui lo si esegue.
Finora abbiamo insistito sull’intero processo che viene turbato per effetto degli spostamenti estrattivi. In effetti il quadro generale che è emerso finora è che, quando un sistema è sottoposto a maggiori sollecitazioni, gli stati osservati perdono simmetria e guadagnano complessità sia spaziale sia temporale. Ma l’esperimento non è finito.
Se il sistema viene ulteriormente sollecitato, appare uno stato dotato di più struttura statistica. Questo stato sembra l’esatto contrario a tutto ciò che pensiamo di aver capito. Esaminiamo più attentamente la sequenza degli eventi.
Perché abbiamo preferito scartare i 90 corpi numerici? Quest’ultimi hanno dei limiti strutturali, quindi per non avere dei limiti adottiamo le 117.480 terzine (
corpo di tre elementi, ma che viaggiano come un corpo unico) che offrono un cammino maggiore per le misurazione. Il carattere di queste misurazione sortisce l’effetto di stabilire una certa distribuzione media delle estrazione, sia per quanto riguarda la loro direzione spaziale, sia per quanto riguarda la loro intensità temporale; qualora venga perturbata, questa distribuzione media tende a ristabilirsi con l’inestricabile complessità del moto della massa estrazionale, dalla loro misurazione si è in grado di distinguere soltanto i valori sotto l’equilibrio di misura statistico, ma uno o al massimo due fra questi si differenziano da tutti gli altri (nel nostro caso solo una si è differenziata)
Nell’esempio soprastante riportato, l’estrazione numero 104 (30/08/2022), evidenzia fra tutte le restanti ruote, solamente la ruota di Venezia e tra le 117.480 terzine, l’unica che avesse un punteggio di 192 e una distribuzione di misura statistica perturbata per i corpi 75-49-73.
Saluti…
